Discrete Negative Binomial Transform1

Introduction

The DiscreteNegativeBinomial transform adapts values from the driver domain to an unbounded integer range, where the weight associated with each range value follows a negative binomial distribution, which is attributed to Blaise Pascal.

The negative binomial distribution enriches Jakob Bernoulli's urn model. The scenario involves an open-ended succession of Bernoulli trials. These trials are independent; that is, the outcome of one trial has no influence upon any other trial, and they are identically distributed, which means that all trials have the same probability p of success. The scenario counts the number k of successful trials until N failures have occurred.

The integers output by DiscreteNegativeBinomial.convert() are controlled by three parameters implemented as Java fields. Field failures is an integer corresponding to the allowed number of failures N in the urn scenario. Field weight is a double-precision number corresponding to the probability of single-trial success p in the urn scenario. This second field ranges from zero (always fails) to unity (always succeeds). Field extent establishes a practical upper limit upon the nominally unbounded output range. This limit is measured in standard deviations. The examples which follow fix extent at 5.

The point density function f(k) is:

f(k) = 
(k+N-1)!
(N-1)!(k)!
 pk(1−p)N

Where the exclamation point indicates factorial. Wikipedia says otherwise about the point density function.2

For the negative binomial family of point density functions, the parametric mean (average, symbolized μ) is given by some sources (including Wikipedia) as Np/(1−p) while the parametric variance (squared deviation, symbolized σ2) is given as Np/(1−p)2.

The graph of the negative binomial distribution starts out with a hump and tails out to zero as values increase. As p grows toward unity, the number of trials expodes while the distinction between consecutive values melts away. The negative binomial distribution thus converges to a gamma distribution, a continuous curve which is also left-bounded at zero, which also starts with a hump, and which also tails out to zero on the right. This gamma distribution has shape parameter N and scale parameter p/(1−p).3

The negative binomial distribution with N=1 is called a geometric distribution. As p grows toward unity, a geometric distribution converges to an exponential distribution (also called "negative exponential") with mean p/(1−p). Geometric is to negative binomial as exponential is to gamma.

Profile

The two panels presented as Figure 1 (a) and Figure 1 (b) illustrate the influence which DiscreteNegativeBinomial.convert() exerts over driver sequences. The horizontal k axis shows the sample values vk which have been obtained from driver values xk using convert(). Each left-side sample graph presents 200 values; the right-side histogram presents a sidewise bar for each range value.

The source sequences used to create Figure 1 (a) and Figure 1 (b) are the same sequences used to create the profile panel for ContinuousUniform, which passes through its driver values undecorated. You can view the actual source sequences by clicking the link. All three source sequences are nominally uniform. The first source is standard randomness from Lehmer. The second source is balanced-bit values from Balance. The third source is an ascending succession produced using DriverSequence.


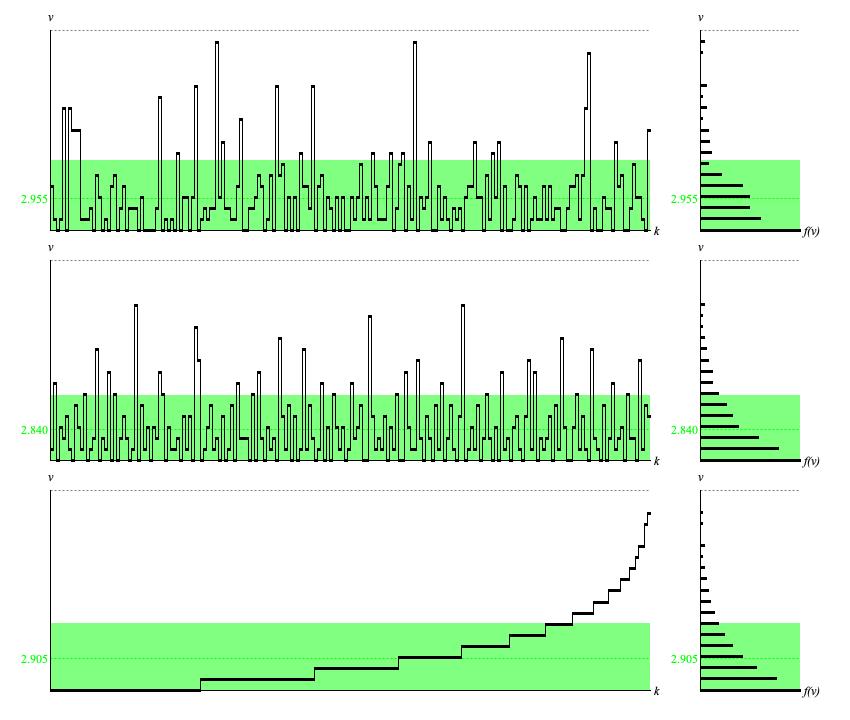
Figure 1 (a): Panel of DiscreteNegativeBinomial output when failures=1 and weight=0.7. Each row of graphs provides a time-series graph of samples (left) and a histogram analyzed from the same samples (right). The first row of graphs was generated using the standard random number generator. The second row was generated using the balanced-bit generator. The third row was generated using an ascending sequence of driver values, equally spaced from zero to unity.

Having failures=1, Figure 1 (a) conforms to a geometric distribution. The vertical v axis in Figure 1 (a) ranges from 0 to 18; that is, the application range from 0 to 17 and the number of outcomes, 18.

For Figure 1 (a) the parametric mean is

μ = Np/(1−p) = 1×0.75/(1−0.75) = 0.75/0.25=3.000.

The parametric deviation is:

σ = √Np/(1−p) = √1×0.75/(1−0.75) = √0.75/0.25 = 3.464.

The standard-random time-series (top row of Figure 1 (b)) bears comparison to the corresponding top-row graphic for DiscreteUniform, which employed the same random source sequence. The relative ups and downs are much alike. The calculated average of 2.955 differs from μ = 3.000 by 1.5%. The calculated deviation of 3.377 around this average differs from σ = 3.462 by 2.4%. However the top-row histogram differs noticably from the bottom-row histogram, which presents ideal point densities.

The balanced-bit time-series (middle row of Figure 1 (a)) likewise bears comparison to the corresponding middle-row graphic for DiscreteUniform, which employed the same balanced-bit source sequence. Again, the relative ups and downs are much alike. The calculated average of 2.840 differs from μ = 3.000 by 5%. The calculated deviation of 3.055 around this average differs from σ = 3.462 by 12%. The middle-row histogram is barely distinguishable from the bottom-row histogram.

The time-series graph generated using ascending, equally spaced driver values (bottom row of Figure 1 (a)) presents the quantile function for the bernoulli distribution with the indicated parameters. This is an irregular ascending step function, where the run of each step indicates the point density and the rise is fixed at one unit. The bottom-row histogram of sample values presents the distribution's probability density function or PDF.

The numerical average of 2.905 differs from μ = 3.00 by 3%. This discrepancy happens because extent=5. Bringing the numerical average up to 2.99 requires increasing extent to 16; however, this would extend the vertical range of the graph up to 55, with few or none of the additional options ever being selected. The numerical standard deviation of 3.181 around this average differs from σ = 3.462 by 8%. Increasing extent to 16 gives a standard deviation of 3.484 and reduces the discrepancy to 0.6%.

The 2.905−3.181 is less than zero, so the light-green shaded interval ranges from 0.00 to 2.905+3.181 = 6.37. Since 6.37/17 = 0.37 = 37% of the full application range from 0 to 17. Since the continuous uniform distribution had 58% of samples within ± one standard deviation of the mean, this suggests that with the negative binomial transform with failures = 1 and weight = 0.75 is squeezing 58% of samples into 37% of the application range, giving a concentration rate of 58/37 = 1.57.


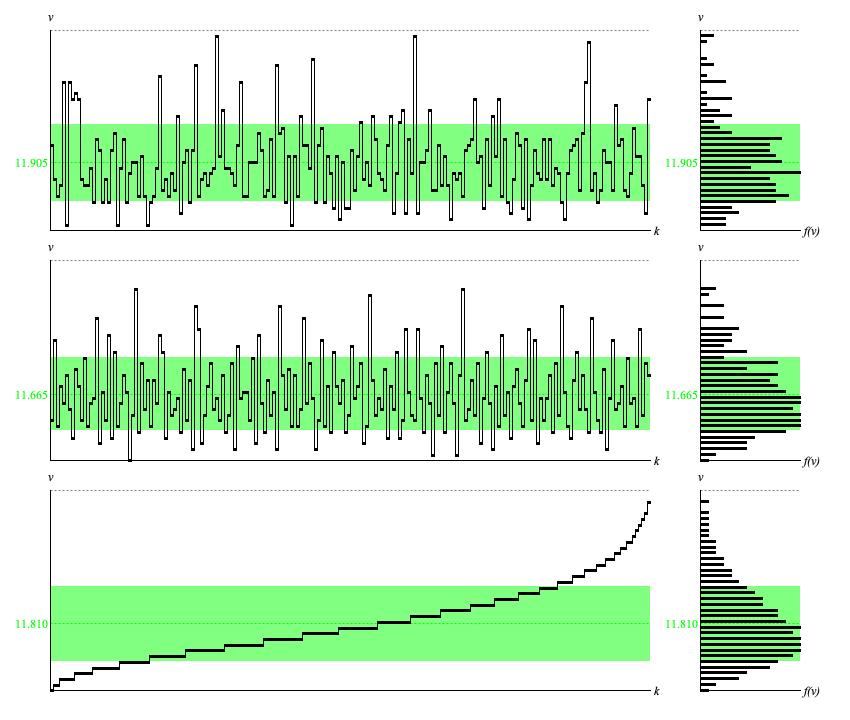
Figure 1 (b): Panel of DiscreteNegativeBinomial output when failures=4 and weight=0.7. Each row of graphs provides a time-series graph of samples (left) and a histogram analyzed from the same samples (right). The first row of graphs was generated using the standard random number generator. The second row was generated using the balanced-bit generator. The third row was generated using an ascending sequence of driver values, equally spaced from zero to unity.

The vertical v axis in Figure 1 (a) ranges from 0 to 38; that is, the application range from 0 to 37 and the number of outcomes, 38.

For Figure 1 (b) the parametric mean is

μ = Np/(1−p) = 4×0.75/(1−0.75) = 3.0/0.25=12.000.

The parametric deviation is:

σ = √Np/(1−p) = √1×0.75/(4−0.75) = √3.0/0.25 = 6.928.

The standard-random time-series (top row of Figure 1 (b)) bears comparison to the corresponding top-row graphic when N = 1. The relative ups and downs are the same. The calculated average of 11.905 differs from μ = 12.000 by 0.8%. The calculated deviation of 6.659 around this average differs from σ6.928 by 4%. However the top-row histogram differs noticably from the bottom-row histogram, which presents ideal point densities.

The standard-random time-series (top row of Figure 1 (b)) bears comparison to the corresponding middle-row graphic when N = 1. The relative ups and downs are the same. The calculated average of 11.665 differs from μ = 12.000 by 2.8%. The calculated deviation of 6.378 around this average differs from σ =  = 6.928 by 8%. The middle-row histogram is barely distinguishable from the bottom-row histogram.

The time-series graph generated using ascending, equally spaced driver values (bottom row of Figure 1 (b)) presents the quantile function for the negative binomial distribution with the indicated parameters. This is an irregular ascending step function, where the run of each step indicates the point density and the rise is fixed at one unit. The bottom-row histogram of sample values presents the distribution's probability density function or PDF.

The numerical average of 11.810 differs from μ = 12.000 by 3%. This discrepancy happens because extent=5. Increasing extent to 16 brings the numerical average up to 11.975 while also extending the vertical range of the graph up to 110. The numerical standard deviation of 6.564 around this average differs from σ = 6.928 by 8%. Increasing extent to gives a standard deviation of 6.860 and reduces the discrepancy to 0.6%.

The interval from 11.810−6.564 = 5.246 to 11.810+6.564 = 18.374 is 2*6.564/37 = 0.355 = 36% of the full application range from 0 to 37. Since the continuous uniform distribution had 58% of samples within ± one standard deviation of the mean, this suggests that the negative binomial transform with failures = 4 and weight = 0.75 is squeezing 58% of samples into 37% of the application range, giving a concentration rate of 58/37 = 1.57. 

/**
 * The {@link DiscreteNegativeBinomial} class implements a discrete statistical
 * transform based on the negative binomial distribution.
 * The negative binomial distribution builds on the notion of the Bernoulli trial
 * described in connection with the {@link DiscreteTrial} transform.  Execute
 * consecutive trials with identical probability p of success.  Repeat the trials
 * until N failures have occurred.  The outcome of the random experiment is
 * the number of successful trials obtained before the Nth failures happens.
 * The {@link #failures} field of the {@link DiscreteNegativeBinomial} class stands
 * in for number of failures N, while the {link weight} field of the the
 * {@link DiscreteTrial} class stands in for the probability of success p.
 * Outcomes from {@link DiscreteNegativeBinomial#convert(double)} are integers
 * ranging from 0 to infinity.  As a statistical transform,
 * {@link DiscreteNegativeBinomial} does not itself employ probability or
 * randomness. Instead it responds to an externally generated driver sequence
 * which may or may not be random. {@link DiscreteDistribution#quantile(double)}
 * converts the driver value to an outcome.
 * @author Charles Ames
 */
public class DiscreteNegativeBinomial extends DiscreteDistributionTransform {
   /**
    * Indicates how many failures must occur before completing the experiment.
    */
   private int failures;
   /**
    * Determines the success rate for individual Bernoulli trials.
    */
   private double weight;
   /**
    * Determines the range extent in standard deviations.
    */
   private double extent;
   /**
    * Constructor for {@link DiscreteNegativeBinomial} instances.
    * @param container An entity which contains this transform.
    */
   public DiscreteNegativeBinomial(WriteableEntity container) {
      super(container);
      this.failures = Integer.MIN_VALUE;
      this.weight = Double.NaN;
      this.extent = Double.NaN;
   }
   /**
    * Setter for {@link #failures}.
    * @param failures The intended {@link #failures} value.
    * @return True if {@link #failures} has changed; false otherwise.
    */
   public boolean setFailures(int failures) {
      checkFailures(failures);
      if (this.failures != failures) {
         this.failures = failures;
         invalidate();
         makeDirty();
         return true;
      }
      return false;
   }
   /**
    * Getter for {@link #failures} .
    * @return The assigned {@link #failures} value.
    * @throws UninitializedException when {@link #failures} has
    * not been initialized.
    */
   public int getFailures() {
      if (Integer.MIN_VALUE == failures)
         throw new UninitializedException("Failures not initialized");
      return failures;
   }
   /**
    * Check if the indicated value is suitable for {@link #failures}.
    * @param failures The indicated value.
    */
   public void checkFailures(int failures) {
      if (0 >= failures)
         throw new IllegalArgumentException("Failures not positive");
   }
   /**
    * Setter for {@link #extent}.
    * @param extent The intended {@link #extent} value.
    * @return True if {@link #extent} has changed; false otherwise.
    */
   public boolean setExtent(double extent) {
      checkExtent(extent);
      if (this.extent != extent) {
         this.extent = extent;
         invalidate();
         makeDirty();
         return true;
      }
      return false;
   }
   /**
    * Getter for {@link #extent} .
    * @return The assigned {@link #extent} value.
    * @throws UninitializedException when {@link #extent} has not
    * been initialized.
    */
   public double getExtent() {
      if (Double.isNaN(extent))
         throw new UninitializedException("Extent not initialized");
      return extent;
   }
   /**
    * Check if the indicated value is suitable for {@link #extent}.
    * @param extent The indicated value.
    */
   public void checkExtent(double extent) {
      if (2. > extent)
         throw new IllegalArgumentException(
            "Extent must exceed two standard deviations");
   }
   /**
    * Getter for {@link #weight} .
    * @return The assigned {@link #weight} value.
    * @throws UninitializedException when {@link #weight} has
    * not been initialized.
    */
   public double getWeight() {
      if (Double.isNaN(weight))
         throw new UninitializedException("Weight not initialized");
      return weight;
   }
   /**
    * Setter for {@link #weight}.
    * @param weight The intended {@link #weight} value.
    * @return True if {@link #weight} has changed; false otherwise.
    */
   public boolean setWeight(double weight) {
      checkWeight(weight);
      if (this.weight != weight) {
         this.weight = weight;
         invalidate();
         makeDirty();
         return true;
      }
      return false;
   }
   /**
    * Check if the indicated value is suitable for {@link #weight}.
    * @param weight The indicated value.
    */
   public void checkWeight(double weight) {
      if (0. > weight || 1. < weight)
         throw new IllegalArgumentException(
            "Weight not in range from zero to unity");
   }
   @Override
   protected void validate(DistributionBase<Integer> distribution) {
      ((DiscreteDistribution) distribution).calculateNegativeBinomial(
         getFailures(), getWeight(), getExtent());

   }
}
Listing 1: The DiscreteNegativeBinomial implementation class.

Coding

The type hierarchy for DiscreteNegativeBinomial is:

DiscreteDistributionTransform embeds a DiscreteDistribution which manages the succession of value-weight items.

Each DiscreteNegativeBinomial instance internally maintains a DiscreteDistribution instance whose succession of items is populated by the call to DiscreteDistribution.calculateNegativeBinomial() in method DiscreteNegativeBinomial.validate(). This call to calculateNegativeBinomial() creates σ×extent items with weights according to the point density function given above.

The distributing step of conversion happens in DiscreteDistributionTransform, where the convert() method does this:

return getDistribution().quantile(driver);

TransformBase maintains a valid field to flag parameter changes. This field starts out false and reverts to false with every time DiscreteNegativeBinomial calls TransformBase.invalidate(). This happens with any change to failures, weight, or extent. Any call to TransformBase.getDistribution() (and DiscreteDistributionTransform.convert() makes such a call) first creates the distribution if it does not already exist, then checks valid. If false, then getDistribution() calls validate(), which is abstract to TransformBase but whose implementation is made concrete by DiscreteNegativeBinomial. And that particular implementation of validate() makes use of DiscreteDistribution.calculateNegativeBinomial(getFailures(), getWeight()), getExtent()) to recalculate the distribution items.

Comments

  1. The present text is adapted from my Leonardo Music Journal article from 1991, "A Catalog of Statistical Distributions". The heading is "Negative Binomial", p. 60.
  2. The formula given by Wikipedia reverses the exponents for p and (1−p). However the value raised to exponent k controls the rate of tail-off, Higher values of p means greater trial success rates, which means that tails should spread out as p increases.
  3. An online paper by Tim Barry, "Gamma, Poisson, and negative binomial distributions" (June 16, 2020) gives the point-density function which I actually use in DiscreteDistribution.calculateNegativeBinomial(). This paper is also my source for the value p/(1−p) given for the gamma distribution's scale parameter.

© Charles Ames Page created: 2022-08-29 Last updated: 2022-08-29