Proximate Randomness: Moderate1
Introduction
The Moderate driver produces sequences which favor smaller sample-to-sample transitions over larger
ones. It imposes a condition of equal probability (like a coin flip) for upward versus downward motion. A second step generates two values uniformly
in the selected region (upward or downward). A third step calculates the absolute distance between the two values and uses this value to determine
how far to transition from the previous value in the selected direction.
What I have named the Moderate driver was developed by
John Myhill as an alternative to the Borel
process.2
The Moderate process is one of several approaches to generating sequences which
exert control over distances between consecutive samples. Others include
Moderate, which John Myhill suggested
as an alternative to Moderate, and
Brownian, where control becomes
parameterized.
Profile
Figure 1 illustrates Moderate output with a sequence of
200 samples generated with a random seed of 1.

Figure 1: Sample output from
Moderate.next(). The left
graph displays samples in time-series while the right graph presents a histogram analyzed from the same samples.
The vertical x axes for both graphs represent the driver domain from zero to unity; the horizontal k axis of the time-series graph (left) plots ordinal sequence numbers; the horizontal f(x) axis of the histogram (right) plots the relative concentration of samples at each point in the driver domain.
Bitwise Analysis
Figure 2 takes the sequence shown in Figure 1 and breaks out what happens in bit 1 (zero or one-half), bit 2 (zero or one-quarter), bit 3 (zero or one-eighth), bit 4 (zero or one-sixteenth), and the residual bits (continuous between zero and one-sixteenth).
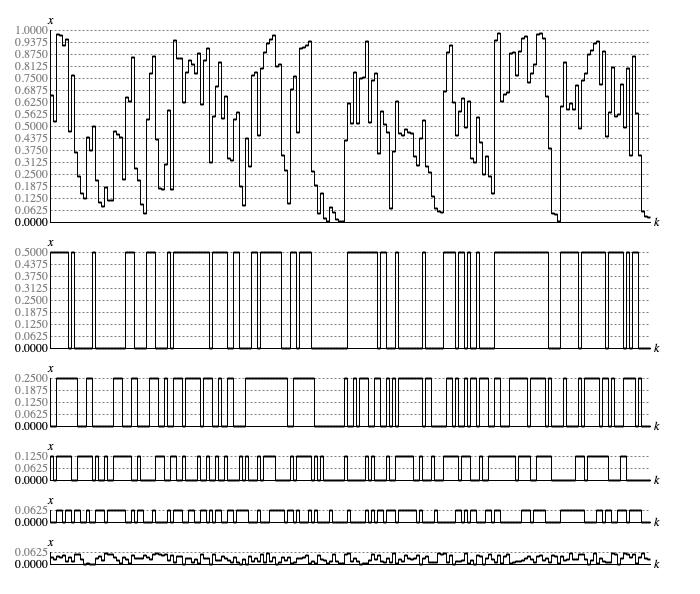
Figure 2: Bitwise analysis of a sequence generated by
Moderate.next().
The bit-specific graphs in Figure 2 transition back and forth between a set state (bit value 1) and a clear state (bit value 0).
Table 1 statistically analyses
of sample the actual stats for these bit-specific graphs. By comparison with the equivalent table for the
Lehmer driver, probability has shifted
away from single samples between transitions toward multiple samples between transitions.
| Transitions | 1 Sample | 2 Samples | 3 Samples | 4 Samples | 5 or more | |
|---|---|---|---|---|---|---|
| Actual Bit 1 | 54 | 37% | 14% | 7% | 12% | 27% |
| Actual Bit 2 | 75 | 37% | 26% | 14% | 6% | 14% |
| Actual Bit 3 | 76 | 43% | 19% | 9% | 7% | 19% |
| Actual Bit 4 | 89 | 42% | 26% | 12% | 7% | 10% |
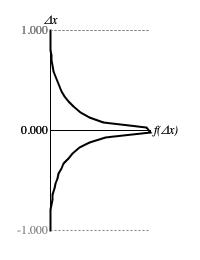
Figure 3: Histogram of sample-to-sample differences from
Moderate.next() after 10,000 consecutive samples.
Transitions
Figure 3 plots the range of sample-to-sample differences along the vertical Δx
axis against the relative concentrations of these values along the horizontal f(Δx) axis.
Compared to the the Borel
driver, concentrations drop more closely to zero, both as Δx approaches -1 from above and as Δx
approaches 1 from below.
The standard deviation of Δx around zero is 0.234, which is well short both of the 0.410 deviation found for the
Lehmer driver and of the 0.353 deviation found for the
Borel driver — an indication of proximity dependence.

Figure 4: Divergence of 4-nibble pattern counts from
Moderate.next() with 10,000 samples per pattern.
Independence
Figure 4 presents a trend graph of histogram tallies for 4-nibble patterns generated using
Moderate.next(). My first attempt to produce this graph following
the methods used for the Lehmer driver flatlined with negligible tallies
at all points. To obtain a nontrivial result it was necessary to limit the graph to the 2049 largest tallies. The most frequent patterns were 0 0 0 0,
and 15 15 15 15, both having an under 1% presence. Following with some 1/3 the maximum
presence were the patterns 1 0 0 0 and 14 15 15 15. These details are consistent with the histogram on the right
side of Figure 2, which has samples concentrating at the bottom and top of the driver range.
The glaring conclusion from Figure 4 is that the Moderate driver
fails the 4-nibble independence test, and does so dramatically.
Moderate implementation class.
Coding
The type hierarchy for Moderate is:
-
DriverBase extends WriteableEntityimplements Driver -
Moderate extends DriverBase
Listing 1 provides the source code for the Moderate
class. The sequential process described at the top of this page is implemented by
generate(), which is not public facing. Instead,
generate() is
called by DriverBase.next().
DriverBase.next() also
takes care to store the new sample in the field
DriverBase.value, where
generate() can employ
DriverBase.getValue() to pick this
(now previous) sample up for the next sample iteration.
DriverBase also offers
setValue() and randomizeValue()
methods to establish the initial sequence value.
Comments
-
The present text is adapted from my Leonardo Music Journal
article from 1992, "A Catalog of Sequence Generators". The discussion occurs
on p. 62, but is missing a heading. Also the
BORELandMODERATEalgorithms were reversed. - John Myhill, "Some Simplifications and Improvements in the Stochastic Music Program".
| © Charles Ames | Page created: 2022-08-29 | Last updated: 2022-08-30 |