Continuous Uniform Transform¹

Introduction

Transform units serve two functions. Their primary function is to adapt the output from a driver unit to whaterver range is appropriate to a specific application. Their secondary function is to influence how values concentrate within various regions of the application range. The ContinuousUniform transform is what you want when range-adaptation is the sole concern, and when you're content to allow whatever distribution the driver values already have to pass through with just rescaling.

The range of values output by ContinuousUniform.convert() is controlled by two parameters implemented as Java fields: minRange and maxRange. These have the restriction that minRange < maxRange.

The convert() method maps a value x in the driver domain from zero to unity into a value v in the application-range from minRange to maxRange using the linear interpolation formula:

Profile

Figure 1 illustrates the influence (or more properly lack of influence) which ContinuousUniform.convert() exerts over driver sequences. The vertical v axis shows the application range, which in this particular instance happens to match the driver range from zero to unity. The horizontal k axis shows the sample values v_k which have been obtained from driver values x_k using convert(). All three source sequences are nominally uniform. Each left-side sample graph presents 200 values; the right-side histogram divides the application range into 20 equal-sized regions. Ideally, this would result in 10 samples per histogram region, but this happens exactly only in the bottom row of graphs.

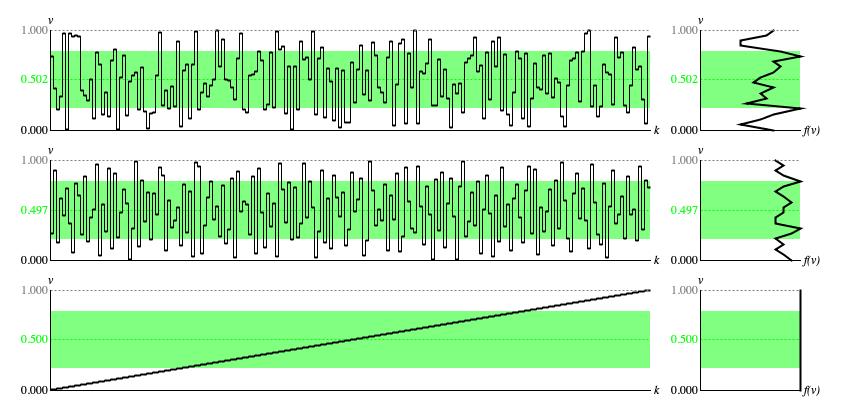
Figure 1: Panel of ContinuousUniform output from three different Driver sources. Each row of graphs provides a time-series graph of samples (left) and a histogram analyzed from the same samples (right). The first row of graphs was generated using the standard random number generator. The second row was generated using the balanced-bit generator. The third row was generated using an ascending sequence of driver values, equally spaced from zero to unity.

The standard random number generator's uniformity manifests only over the long term; its concern for the independence of consecutive samples works against short-term uniformity. The standard-randomness histogram appearing in the top row of Figure 1 is hardly uniform, though the white space separating the vertical v axis from the smallest f(v) value is about the same as the horizontal distance separating the smallest f(v) value from the largest f(v) value. Besides, no other distribution suggests itself.

The balanced-bit generator (middle row of Figure 1) actively strives for uniformity over the short term. The balanced-bit histogram appearing in Figure 1 has half again the distance from the smallest f(v) value to the largest f(v) value.

There is no surer way of obtaining uniform driver values than to calculate an increment Δx = 1/N, where N is the number of samples. The first sample value x₀ is set to Δx/2; subsequent values are calculated as x_k = x_k-1 + Δx until x_k threatens to exceed unity. With driver values generated in this manner, the graphs in the bottom row of Figure 1 come to resemble two essential functions describing the Transform unit's underlying statistical distribution: The time-series graph of samples comes to resemble the distribution's percentile function, which for a continuous uniform distribution is an upward sloping line. The histogram of sample values comes to resemble the distribution's probability density function, which for a continuous uniform distribution is constant.

For each graph in Figure 1 the average sample value is plotted as a dashed green line, while the interval between ± one standard deviation around the average is filled in with a lighter green background. For the ideally uniform driver values plotted in the third row of graphs, the average sample value is 0.5 and the standard deviation is 0.289. The interval from 0.5-0.289 to 0.5+0.289 is 2*0.289 = 0.58 = 58% of the full application range from zero to unity; since sequence is uniform and the transform passes this uniformity along, we can assert that 58% of samples fall within the green-shaded part of the graph, giving a concentration rate of 58/58 = 1.00.

/**
 * The {@link ContinuousUniform} class implements a {@link Transform}
 * which adapts the driver range from zero to unity to a bounded range.
 * The minimum and maximum range bounds are managed by the
 * {@link BoundedTransform} superclass.  Whatever distribution
 * characterizes the driver values passes through except for being
 * scaled to the range bounds.
 * @author Charles Ames
 */
public class ContinuousUniform extends BoundedTransform {
   /**
    * Constructor for {@link ContinuousUniform} instances.
    * @param container An entity which contains this transform.
    */
   public ContinuousUniform(WriteableEntity container) {
      super(container);
   }
   @Override
   public Double convert(double driver) {
      return interpolate(driver);
   }
}

Comments

1. The present text is adapted from my Leonardo Music Journal article from 1991, "A Catalog of Statistical Distributions". The heading is "Continuous Uniform", p. 62.