Iterating Lookup Indices: IndexSequence

Introduction

Instances of IndexSequence class generate sequences of integers by drawing values sequentially from a stored list. Values range from 0 to limit-1, where limit should match the size of the external array or list from which supply elements are to be drawn. The list embedded as IndexSequence.values is something distinct from the external supply.

The Sequence.UsageMode enumeration identifies four ways of using IndexSequence (and also four ways of using DriverSequence, but these have different implications).

• UsageMode.UNIQUE_DIRECT stores indices one-for-one to each supply element, and maintains them in order from 0 to limit-1. This is the most rudimentary mode. The supply takes responsibilty both for (original) order and for content. When the samplingOffset is 0 and the samplingIncrement is 1, IndexSequence corresponds to the SEQUENCE selection principle of Koenig's Project2. When the samplingOffset is -1 and the samplingIncrement is -1, IndexSequence generates indices in reverse order (retrograde).
• UsageMode.UNIQUE_SHUFFLED also stores indices one-for-one to each supply element. Although indices range from 0 to limit-1, their presentation order is shuffled randomly prior to each new cycle. The supply takes responsibilty for content, while the indexer ensures that this content is fully expressed over a cycle. In practice, samplingOffset should always be 0, while samplingIncrement should always be 1 (nothing else makes sense owing to shuffling). In this mode with these settings, IndexSequence corresponds to the SERIES selection principle of Koenig's Project2.
• UsageMode.SAMPLES_DIRECT stores indices ranging from 0 to limit-1. In this mode the indexer takes responsibility for order while the supply takes responsibilty for content. Hence the number of stored indices is typically larger than limit, making duplicates inevitable. The supply is typically duplicate free; elements being arranged in whatever passes for an ascending succession. When the samplingOffset is 0 and the samplingIncrement is 1, IndexSequence presents indices in forward order (original). When the samplingOffset is -1 and the samplingIncrement is -1, IndexSequence generates indices in reverse order (retrograde).
• UsageMode.SAMPLES_SHUFFLED stores indices ranging from 0 to limit-1 but shuffles their presentation order at the beginning of each new cycle. In this mode the supply takes responsibilty for unique content, but if a certain index has duplicates the corresponding element will recur that many times over the extent of a cycle. Since order otherwise makes no difference, indices should be added in ascending order, with duplicates grouped. The supply is typically duplicate free; elements being arranged in whatever passes for an ascending succession. In practice, samplingOffset should always be 0, while samplingIncrement should always be 1. In this mode with these settings, IndexSequence corresponds to the RATIO selection principle of Koenig's Project2. (The RATIO algorithm is different, though equivalent in effect).

Profile

Figure 1 illustrates four examples of IndexSequence output with sequences of 96 samples generated. All four examples were generated with 8 cycles, each with 12 samples. The random seed was 2, which produced a prettier shape for UsageMode.SAMPLE_DIRECT than seed value 1.

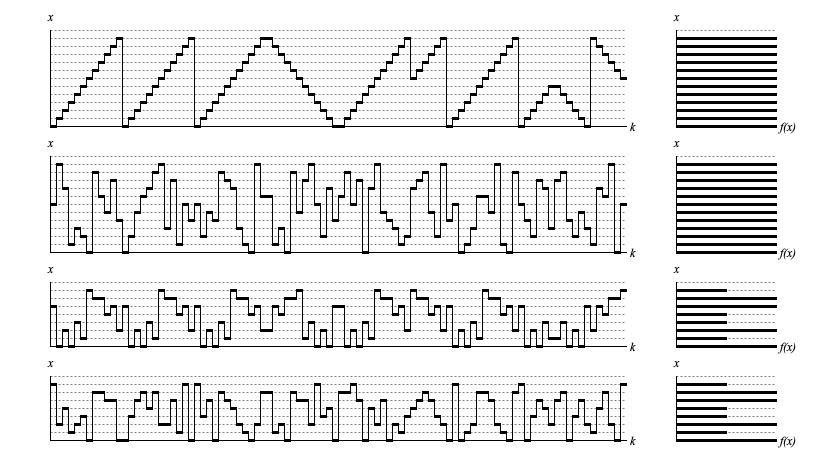
Figure 1: Sample output from IndexSequence.next() with different usage modes. The left graph in each row displays samples in time-series while the right graph in the same row presents a histogram analyzed from the same samples.

The vertical x axes for the two graphs in each row represent the index domain from zero to N; the horizontal k axis of the time-series graph (left) plots ordinal sequence numbers; the horizontal f(x) axis of the histogram (right) plots the relative concentration of samples at each point in the driver domain.

The topmost graph was generated with UsageMode.UNIQUE_DIRECT. The stored collection was populated with index values from 0 to 11 (12 in all). The first three cycles employed a sampling offset of 0 (start with leftmost stored value) and a sampling increment of 1 (advance rightward by single elements). The fourth cycle employed offset -1 (start with rightmost stored value) and increment of -1 (advance leftward by single elements). The fifth cycle reprised offset 0 and increment 1. The sixth and seventh cycle employed offset 5 (start with rightmost value in first half of collection) and increment -1 (advance leftward by single elements). The eighth and final cycle employed offset 6 (start with second half of collection) and increment 1 (advance rightward by single elements). The histogram on the far right was generated with a granualarity equal to the collection length. Since collection values are equally spaced, and since each stored value occurs a total of eight times during the overall sequence, the histogram flatlines.

The second-from graph was generated with UsageMode.UNIQUE_SHUFFLE. The stored collection was also populated with index values from 0 to 11; however this mode shuffles the order of these values at the beginning of each cycle. Although this presentation order changes, it remains true that each stored value occurs a total of eight times during the overall sequence. Hence the histogram flatlines for this sequence as well.

The third-from-top graph was generated with UsageMode.SAMPLE_DIRECT. Here an array containing the index values {0, 0, 1, 2, 2, 3, 4, 5, 5, 6, 6, 7} was shuffled giving {5, 0, 2, 0, 3, 1, 7, 6, 6, 4, 5, 2}, then loaded into the stored collection. The first three cycles employed a sampling offset of 0 (start with leftmost stored value) and a sampling increment of 1 (advance rightward by single elements). The fourth cycle employed offset -1 (start with rightmost stored value) and increment of -1 (advance leftward by single elements). The fifth cycle reprised offset 0 and increment 1. The sixth and seventh cycle employed offset 5 (start with rightmost value in first half of collection) and increment -1 (advance leftward by single elements). The eighth and final cycle employed offset 6 (start with second half of collection) and increment 1 (advance rightward by single elements). This time around the histogram granualarity remains at 12 but the number of distinct values has dropped to 8; thus, the histogram drops to zero in four places. Also, since values 0, 2, 5, and 6 have duplicates each recurs sixteen times during the overall sequence, while values 1, 3, 4, and 7 only recur eight times. The histogram is by no means flat.

The bottommost graph was generated with UsageMode.SAMPLE_SHUFFLE. Here the array containing the index values {5, 0, 2, 0, 3, 1, 7, 6, 6, 4, 5, 2} was loaded into the stored collection; however this original ordering is never seen because this mode shuffles the order at the beginning of each cycle. In spite of the shuffling, it remains true that values 0, 2, 5, and 6 recur sixteen times, while values 1, 3, 4, and 7 only recur eight times. Thus the bottommost histogram exactly matches the third-from-top histogram.

Short-Term Uniformity

Output from IndexSequence, with UsageMode.UNIQUE_SHUFFLE selected, bears a particular relation to the Lehmer driver when coupled with the DiscreteUniform transform. Understand that Lehmer wraps Java's standard random number generator. Output from IndexSequence and also from Lehmer|DiscreteUniform nominally follows a discrete uniform distribution; however of the two approaches, only IndexSequence realizes this distribution over the short term. In that sense Lehmer|DiscreteUniform implements the urn model's selection with replacement, just as IndexSequence implements selection without replacement.

This mode of output from IndexSequence is comparable to output from Feedback with equally weighted range values. The difference is how these two indexers get to short-term uniformity. When the number of samples N making up a cycle or frame is known in advance, UNIQUE_SHUFFLE will produce a sequence of samples which is perfectly uniform, in the sense of having the flattest possible histogram. However such perfect conformity is also achievable by Feedback with a heterogeneity setting of 0.1.

Feedback employs a quasi-deterministic algorithm which actively seeks to place new samples in less-populated intervals. The nature of this algorithm is such that not only will an N-sample frame be very nearly uniform, both the first and second halves of the frame will also be very nearly uniform. By contrast, with IndexSequence in UsageMode.UNIQUE_SHUFFLE the halves of the frame will very likely not be uniform. For example, shuffling could place a preponderance of smaller indices in the first half, then compensate with a preponderance of larger indices in the second half.

/**
 * Instances of the {@link IndexSequence} class iterate through a stored
 * collection of integers.
 * @author Charles Ames
 */
public class IndexSequence
extends Sequence<Integer> implements Indexer {
   int limit;
   /**
    * Constructor for {@link IndexSequence} instances.
    * @param container A {@link WriteableEntity} which contains
    * this indexer.
    */
   public IndexSequence(WriteableEntity container) {
      super(container);
      this.limit = Integer.MIN_VALUE;
   }
   /**
    * Constructor for {@link Balance} instances without container.
    */
   public IndexSequence() {
      this(null);
   }
   /**
    * Getter for {@link #limit}.
    * @return The assigned {@link #limit} value.
    * @throws UninitializedException when the limit has not been initialized.
    */
   public int getLimit() {
      if (Integer.MIN_VALUE == limit)
         throw new UninitializedException("Limit not initialized");
      return limit;
   }
   /**
    * Setter for {@link #limit}.
    * @param limit The intended {@link #limit} value.
    * @throws IllegalArgumentException when the limit is not positive.
    */
   public void setLimit(int limit) {
      if (0 >= limit)
         throw new IllegalArgumentException("Limit not positive");
      this.limit = limit;
   }
   @Override
   public void addValue(Integer value) {
      Indexer.checkIndexValue(value, Integer.MAX_VALUE);
      super.addValue(value);
   }
   /**
    * Append the members collection from a {@link Permutation} instance
    * to the {@link Sequence#values} collection.
    * This method leverages {@link Permutation#iterateMembers(int, int, int, int)},
    * whose documentation further explains the start, increment, multiplier, and
    * transposition arguments.
    * @param permutation The source {@link Permutation} instance.
    * @param start Starting position.
    * @param increment Position increment between iterations.
    * @param multiplier Multiplier applied modulo N to each member.
    * @param transposition Offset added modulo N to each member.
    * @throws UnsupportedOperationException when {@link Sequence#values}
    * already contains elements.
    * @throws UnsupportedOperationException when iteration from
    * {@link Sequence#values} is in progress.
    */
   public void fillValues(Permutation permutation,
         int start, int increment, int multiplier, int transposition) {
      if (0 != itemCount())
         throw new UnsupportedOperationException("Values already populated");
      Iterator<Integer> iterator
         = permutation.iterateMembers(start, increment, multiplier, transposition);
      while (iterator.hasNext()) {
         super.addValue(iterator.next());
      }
   }
   @Override
   public void fillAscending(int itemCount) {
      setLimit(itemCount);
      if (0 >= itemCount)
         throw new IllegalArgumentException("Size must be positive");
      if (0 != itemCount())
         throw new UnsupportedOperationException("Values already populated");
      for (int index = 0; index < itemCount; index++) {
         addValue(index);
      }
   }
   /**
    * Fill the {@link Sequence#values} collection with {@code itemCount} indices
    * generated automatically.
    * @param itemCount The intended size of the {@link Sequence#values} collection.
    * @param generator The index generator.
    * @throws IllegalArgumentException when the size argument is not positive.
    * @throws UnsupportedOperationException when iteration from {@link Sequence#values}
    * is in progress.
    */
   public void autoFillValues(int itemCount, Indexer generator) {
      if (0 >= itemCount)
         throw new IllegalArgumentException("Size must be positive");
      if (0 != itemCount())
         throw new UnsupportedOperationException("Values already populated");
      for (int index = 0; index < itemCount; index++) {
         if (!generator.hasNext()) break;
         addValue(generator.next());
      }
   }
   @Override
   public double minGraphValue() {
      int result = Integer.MAX_VALUE;
      for (int index : getValues()) {
         if (index < result) result = index;
      }
      if (Integer.MAX_VALUE == result)
         throw new UnsupportedOperationException("Empty sequence");
      return result;
   }
   @Override
   public double maxGraphValue() {
      int result = Integer.MIN_VALUE;
      for (int index : getValues()) {
         if (index > result) result = index;
      }
      if (Integer.MIN_VALUE == result)
         throw new UnsupportedOperationException("Empty sequence");
      return result;
   }
   @Override
   protected void checkValue(Integer value) {
      Indexer.checkIndexValue(value, getLimit());
   }
   @Override
   protected int compareValues(Number a, Number b) {
      int d = ((Integer) a) - ((Integer) b);
      if (d > 0) return 1;
      if (d < 0) return -1;
      return 0;
   }
}