Design III: Contours

Introduction

The contour package described on this page implements mathematical functions mapping ordinates to abscissas. Contours are piecewise continuous which means that they are made up of contiguous segments; abrupt discontinuities are permitted at segment boundaries, but within a segment values must either remain constant, or they must progress smoothly from an origin to a goal.

Ordinates are also described either as independent variables, or more succinctly as inputs. Ordinates draw from domains which are effectively continuous, specifically the real numbers (represented in Java using the double data type) or the rational numbers (represented in my own programs using a Ratio class). The package described here was originally developed for a program which interprets text encodings of musical scores into an object model suitable for export to MIDI, MusicXML, and MUSIC-N. I have since incorporated them as a feature of my own digital sound synthesis package (based on MUSIC-N). More pertinent to the topic of sequence generation, I have employed this package in my own composing programs, where they realize profiles controlling how pieces evolve. Contour ordinates are very often moments of time; however, the density to timbre-weight mappings of Xenakis's Stochastic Music Program illustrate one of many alternative roles.

Abcissas are also described as dependent variables or outputs. Contour abcissas can be of arbitrary types, however only double or collections of double can take advantage of interpolation between an origin and a goal.

My Contour interface is presented below as Listing 1. Contour instances manage lists of child instances implementing the Segment interface. The child interface is encapsulated within the parent (scroll down to the bottom of Listing 1). Each each segment is bounded below by a left ordinate which maps to an origin abcissa, and each segments bounded above by a right ordinate which maps to a goal abcissa. Segments are required to be contiguous, that is, if a segment has a successor, then the successor's left ordinate must match the original segment's right ordinate.

Interpolation Modes

Within a Contour instance, abcissa values for ordinates between left and right are determined by a calculationMode associated with the parent Contour instance. Options for calculationMode property are provided by the Contour interface's CalculationMode enumeration, which is included in Listing 1. There are five calculation modes:


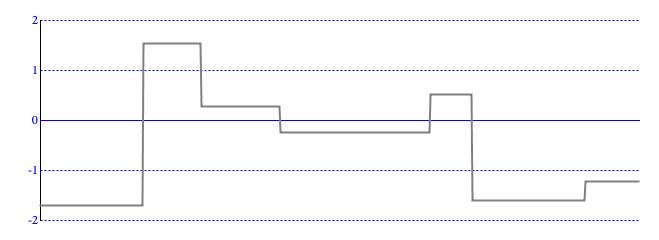
Figure 1: A DISCRETE contour is a succession of segments, each presenting a constant value.

Discrete Segments

The DISCRETE calculation mode (Figure 1) undertakes no interpolation, so is available for any type of abcissa.


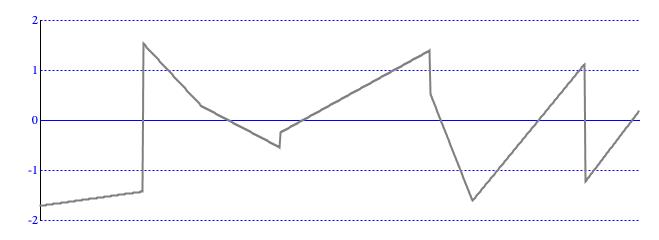
Figure 2: A LINEAR contour is a succession of segments, each presenting a straight line from a designated origin to a designated goal.

Linear Segments

The LINEAR calculation mode (Figure 2) undertakes standard linear interpolation.

Let y(x) be the interpolation factor calculated as:

y(x) =  (
x - left
right - left
 )

Then the interpolated contour value f(x) for ordinate x is calculated as:

f(x) = origin + (goal - origin)*y(x).

f(x) could alternatively be calculated as:

f(x) = M(x - left) + origin.

Where the slope M is constant everywhere within the segment:

M =  (
goal - origin
right - left
 )

Either of these calculations makes sense only when the abcissa is of a continuous numeric type such as double or when the abcissa is a collection of such numbers.

A mathematical function is said to be linear when its slope is everywhere constant. Linearity also means this: Let x0, x1, … xN be a sequence of ordinates equally spaced with distance Δx, with x0 fixed at the left ordinate, and with xN fixed at the right ordinate. Let f(x) be the interpolated contour value for ordinate x. Then in all cases,

f(xk+Δx) - f(xk) = MΔx.

Putting this math into words, when the ordinate moves in equal increments, then the corresponding contour values also move in equal increments.


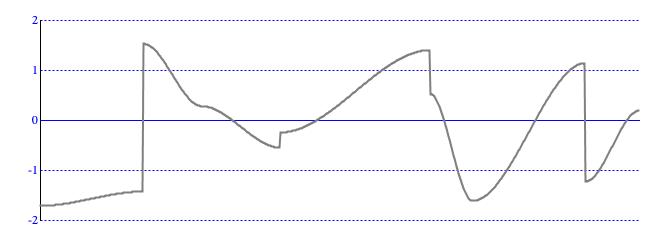
Figure 3: A SPLINE contour is a succession of segments, each presenting a smooth curve which starts out horizontally from a designated origin, bends toward a designated goal, then bends back to horizontal before the goal is reached.

Spline Segments

The LINEAR calculation mode (Figure 3) undertakes spline interpolation. The slope of the resulting curve is zero (horizontal) both leaving the origin and approaching the goal. At the midpoint of the segment the curve approximates the linear-interpolation line with slope M given previously.

(goal - origin)/(right - left).


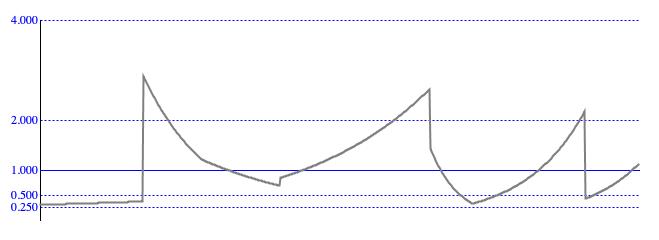
Figure width="50%" 4: An EXPONENTIAL contour is a succession of segments, each presenting an "equal ratios" curve from a designated origin to a designated goal.

Exponential Segments

The EXPONENTIAL calculation mode (Figure 4) undertakes exponential interpolation.

Let y(x) be the interpolation factor calculated as:

y(x) =  (
x - left
right - left
 )

When the goal is greater than the origin, then the interpolated contour value f(x) for ordinate x is calculated as

f(x) = origin *  (
goal
origin
 ) y(x)

When the goal is less than the origin, then the interpolated contour value f(x) for ordinate x is calculated as

f(x) = goal *  (
origin
goal
 ) 1-y(x)

Since there is no way of obtaining a non-positive number by raising any double to any power, origins and goals have the additional requirement of being positive.

Once again, let x0, x1, … xN be a sequence of ordinates equally spaced with distance Δx, with x0 fixed at the left ordinate, and with xN fixed at the right ordinate. Let f(x) be the interpolated contour value for ordinate x. Then in all cases,

f(xj + Δx)
f(xj)
  = 
f(xk + Δx)
f(xk)

Putting this math into words, when the ordinate moves in equal increments, then the corresponding contour values move in equal ratios.1


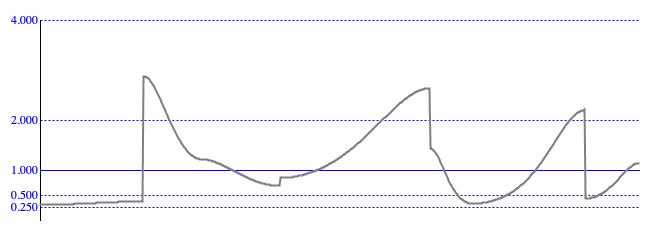
Figure 5: A SPLINEX contour is a succession of segments, each nominally following an "equal ratios" curve. However the curve bends to horizontal both leaving the origin and approaching the goal.

SplineX Segments

SPLINEX is illustrated in Figure 5. Since piecewise linear contours have spline variants, and since exponential contours are linear contours raised to a power, then it is reasonable that exponential contours should also have spline variants. I introduced the SPLINEX option to control sound-synthesis frequencies, motivated by the as-yet-untested suspicion that 2nd-order discontinuities (when a contour doesn't break, but does make a sharp turn) might introduce pops.

Editing Segments

In all applications the train of Segment instances should be well formed, meaning that for any two consecutive segments in the list, the right ordinate of the first segment must always coincide with the left ordinate of the second segment. That way it is always clear what the defined range of ordinates valid is, and exactly which segment pertains to any given valid ordinate.

One design consideration for this package was whether the Segment instances should be fixed as initially described or should be editable. The downside to enabling segment editing is that what the contours are describing may not be alterable; for example, if the contour ultimately determines the profile for a continuous control in MIDI, or in software sound synthesis. Another downside is all the complication:

These complications are simply justifications for working it through myself so that others won't have to. The clincher for me was this: there's a more efficent (from the end user's perspective) and intuitive way of describing segments than tablizing left ordinates, right ordinates, origins, and goals.

This more intuitive approach was first demonstrated in the early 1970's Linear Music Code of Alan Ashton, and it takes advantage of the fact that when one is encoding a score, one always knows where in time (i.e. at what beat of what measure) one is. So the encoder can indicate, at the present moment, 'let the tempo be this', or 'let the dynamic be that'. So much for origins. For goals you need an additional fact: how long does the transition take? Here the encoder can indicate, at the present moment, 'over the next two 4-4 measures (a whole note × 2) accelerate from whatever the tempo is now to this new faster tempo', or 'over the next dotted half note increase the dynamic gradually from whatever the dynamic is now to that louder dynamic'.

Ashton's approach assumes that the contour is being built on the fly, from left to right, that each new origin extends tentatively out to infinity until time comes along to describe the next segment. That requires segments to be dynamically editible rather than fixed. It also requires infinity to be considered a valid right bound for new segments.

Coding

My contour package implements a single-tier composite design pattern where a single parent object implementing the Contour interface (Listing 1) stands for the whole, while multiple child objects implementing the Segment interface (bottom of Listing 1) detail the parts. Package consumers typically interact with the parent only: they define a contour's content by calling Contour.createSegment(left, right, origin, goal) and they translate ordinates into abcissas by calling Contour.valueAt(ordinate). An exception to only contour-only access would be for a graphic editor, which would need segment details in order to render graphs efficiently. However, bypassing createSegment() can seriously break things, so this needs to be prevented. 

/**
 * A {@link Contour} maps a generic ordinate (independent variable) to
 * an abscissa (dependent variable) which is also generic, but which
 * will often be a double-precision number.  The right (upper) ordinate
 * bound of one segment always coincides with the left (lower) ordinate
 * bound of its successor.
 * An example of a double-precision ordinate is time, measured in
 * seconds. An example of a {@link Ratio} ordinate is duration, measured
 * in whole notes. Contour values are continuous within each segment,
 * but values may change abruptly at segment boundaries.
 * @author Charles Ames
 * @param <S> Ordinate class (left and right bounds)
 * @param <T> Abscissa class (origins and goals)
 */
public interface Contour<S extends Comparable<S>, T extends Comparable<T>> {
   /**
    * The {@link CalculationMode} determines how given an ordinate
    * within a segment, the value of the contour is calculated using the
    * segment's left bound, right bound, origin, and goal.
    * @author Charles Ames
    */
   enum CalculationMode {
      /**
       * The value of the contour at any ordinate within the segment is
       * the same as the segment origin.
       */
      DISCRETE {
         @Override
         public double calculate(double ordinate,
               double left, double right, double origin, double goal) {
            checkOrdinate(ordinate, left, right);
            return origin;
         }
         @Override
         public double areaBetween(double ord1, double ord2,
               double left, double right, double origin, double goal) {
            checkOrdinate(ord1, left, right);
            checkOrdinate(ord2, left, right);
            double duration = ord2 - ord1;
            if (duration < 0.) {
               throw new IllegalArgumentException("Ordinates out of order");
            }
            return origin * duration;
         }
         @Override
         public double areaBetweenInvert(double ord1, double ord2,
               double left, double right, double origin, double goal) {
            checkOrdinate(ord1, left, right);
            checkOrdinate(ord2, left, right);
            double duration = ord2 - ord1;
            if (duration < 0.) {
               throw new IllegalArgumentException("Ordinates out of order");
            }
            return duration / origin;
         }
      },
      /**
       * The value of the contour at any ordinate within the segment is
       * linearly interpolated, based on where the ordinate falls within
       * the segment's left and right boundaries.
       */
      LINEAR {
         @Override
         public double calculate(double ordinate,
               double left, double right, double origin, double goal) {
            checkOrdinate(ordinate, left, right);
            if (MathMethods.haveSmallDifference(origin, goal)) {
               return origin;
            }
            double t = getInterpolationFactor(ordinate, left, right);
            return origin + t * (goal - origin);
         }
         @Override
         public double areaBetween(double ord1, double ord2,
               double left, double right, double origin, double goal) {
            checkOrdinate(ord1, left, right);
            checkOrdinate(ord2, left, right);
            double duration = ord2 - ord1;
            if (duration < 0.) {
               throw new IllegalArgumentException("Ordinates out of order");
            }
            double y1 = calculate(ord1, left, right, origin, goal);
            double y2 = calculate(ord2, left, right, origin, goal);
            return (y1 + y2) * 0.5 * duration;
         }
      },
      /**
       * The value of the contour at any ordinate within the segment is
       * exponentially interpolated, based on where the ordinate falls
       * within the segment's left and right boundaries. The origin and
       * goal of any segment must both be positive numbers.
       */
      EXPONENTIAL {
         @Override
         public double calculate(double ordinate,
               double left, double right, double origin, double goal) {
            checkOrdinate(ordinate, left, right);
            if (MathMethods.haveSmallDifference(origin, goal)) {
               return origin;
            }
            double t = getInterpolationFactor(ordinate, left, right);
            if (origin < goal ) {
               return origin * Math.pow(goal/origin, t);
            }
            else {
               return goal * Math.pow(origin/goal, 1. - t);
            }
         }
      },
      /**
       * The value of the contour at any ordinate within the segment
       * from a to b is interpolated using a spline function q(x)
       * where q'(a)=0 and q'(b)=0.
       */
      SPLINE {
         @Override
         public double calculate(double ordinate,
               double left, double right, double origin, double goal) {
            checkOrdinate(ordinate, left, right);
            if (MathMethods.haveSmallDifference(origin, goal)) {
               return origin;
            }
            double t = getSplineFactor(ordinate, left, right);
            return origin + t * (goal - origin);
         }
      },
      /**
       * The value of the contour at any ordinate within the segment from
       * a to b is interpolated using an exponential-spline function
       * pow(a,q(x)) where q'(a)=0 and q'(b)=0.
       */
      SPLINEX {
         @Override
         public double calculate(double ordinate,
               double left, double right, double origin, double goal) {
            checkOrdinate(ordinate, left, right);
            if (MathMethods.haveSmallDifference(origin, goal)) {
               return origin;
            }
            if (goal > origin) {
               return origin * Math.pow(goal / origin,
                     getSplineFactor(ordinate, left, right));
            }
            else {
               return goal * Math.pow(origin / goal,
                     1.-getSplineFactor(ordinate, left, right));
            }
         }
      };
      /**
       * Calculate a value intermediate between origin and goal, based on an
       * ordinate ranging from left to right.
       * @param ordinate The ordinal position between left and right.
       * @param left The lower bound for the ordinate.
       * @param right The upper bound for the ordinate.
       * @param origin The function value as of the leftmost ordinate.
       * @param goal The function value as of the rightmost ordinate.
       * @return The calculated function value.
       */
      public abstract double calculate(double ordinate,
            double left, double right, double origin, double goal);
      /**
       * Verify that the indicated ordinate falls within the segment range.
       * @param ordinate The indicated ordinate.
       * @param left Lower ordinate bound.
       * @param right Upper ordinate bound.
       * @throws IllegalArgumentException when the ordinate falls short
       * of left or falls long of right.
       */
      public void checkOrdinate(double ordinate, double left, double right) {
         if (left > ordinate || ordinate > right) {
            throw new IllegalArgumentException("Ordinate [" + ordinate
                  + "] out of range from "
                  + MathMethods.formatDouble(left, 4) + " to "
                  + MathMethods.formatDouble(right, 4));
         }
      }
      /**
       * Scale the distance from the left ordinate to the indicated
       * ordinate by the segment width.
       * @param ordinate A value ranging from the first segment start
       * time to the last segment .
       * @param left Lower ordinate bound.
       * @param right Upper ordinate bound.
       * @return The distance from the left ordinate to the indicated
       * ordinate, scaled by the segment width.
       * @throws IllegalArgumentException when the ordinate falls short
       * of left or falls long of right.
       */
      public final double getInterpolationFactor(double ordinate,
            double left, double right) {
         double width = right - left;
         if (ContourFromReal.MAX_ORDINATE <= width) return 0;
         return (ordinate - left) / width;
      }
      /**
       * Calculate a spline value for the indicated ordinate.
       * The spline function is a 3rd-order polynomial g(x) where
       * g'(left) = 0 and g'(right) = 0;
       * Formula source: https://en.wikipedia.org/wiki/Spline_interpolation#Algorithm_to_find_the_interpolating_cubic_spline
       * @param ordinate A value ranging from left to right.
       * @param left The lower bound for the ordinate.
       * @param right The upper bound for the ordinate.
       * @return A spline value ranging from zero to unity.
       * @throws IllegalArgumentException when the ordinate falls short
       * of left or falls long of right.
       */
      public final double getSplineFactor(double ordinate,
            double left, double right) {
         double t = getInterpolationFactor(ordinate, left, right);
         return 3.0*t*t - 2.0*t*t*t;
      }
      /**
       * Get the area under the contour between two ordinates
       * @param ord1 The starting ordinate.
       * @param ord2 The ending ordinate.
       * @param left The lower bound for both the starting ordinate
       * and the ending ordinate.
       * @param right The upper bound for both the starting ordinate
       * and the ending ordinate.
       * @param origin The function value as of the leftmost ordinate.
       * @param goal The function value as of the rightmost ordinate.
       * @return The calculated area.
       */
      public double areaBetween(double ord1, double ord2,
            double left, double right, double origin, double goal) {
         checkOrdinate(ord1, left, right);
         checkOrdinate(ord2, left, right);
         double duration = ord2 - ord1;
         if (duration < 0.) {
            throw new IllegalArgumentException("Start time exceeds end time");
         }
         double y1 = calculate(ord1, left, right, origin, goal);
         double y2 = calculate(ord2, left, right, origin, goal);
         return area(ord1, ord2, y1, y2, left, right, origin, goal);
      }
      // Recursive helper for areaBetween()
      private double area(double ord1, double ord2, double y1, double y2,
            double left, double right, double origin, double goal) {
         double r = Math.abs(Math.log(y2 / y1));
         double result;
         if (r < .05) {
            result = (y1 + y2) * 0.5 * (ord2-ord1);
         }
         else {
            double x = 0.5*(ord1+ord2);
            double y = calculate(x, left, right, origin, goal);
            result = area(ord1, x, y1, y, left, right, origin, goal)
                  + area(x, ord2, y, y2, left, right, origin, goal);
         }
         return result;
      }
      /**
       * Get the area under the inverted contour between two ordinates
       * @param ord1 The starting ordinate.
       * @param ord2 The ending ordinate.
       * @param left The lower bound for both the starting ordinate
       * and the ending ordinate.
       * @param right The upper bound for both the starting ordinate
       * and the ending ordinate.
       * @param origin The function value as of the leftmost ordinate.
       * @param goal The function value as of the rightmost ordinate.
       * @return The calculated area.
       */
      public double areaBetweenInvert(double ord1, double ord2,
            double left, double right, double origin, double goal) {
         checkOrdinate(ord1, left, right);
         checkOrdinate(ord2, left, right);
         double duration = ord2 - ord1;
         if (duration < 0.) {
            throw new IllegalArgumentException("Start time exceeds end time");
         }
         double y1 = 1./calculate(ord1, left, right, origin, goal);
         double y2 = 1./calculate(ord2, left, right, origin, goal);
         return areaInvert(ord1, ord2, y1, y2, left, right, origin, goal);
      }
      // Recursive helper for areaBetweenInvert()
      private double areaInvert(double ord1, double ord2, double y1, double y2,
            double left, double right, double origin, double goal) {
         double r = Math.abs(Math.log(y2 / y1));
         double result;
         if (r < .05) {
            result = (y1 + y2) * 0.5 * (ord2-ord1);
         }
         else {
            double x = 0.5*(ord1+ord2);
            double y = 1./calculate(x, left, right, origin, goal);
            result = areaInvert(ord1, x, y1, y, left, right, origin, goal)
                  + areaInvert(x, ord2, y, y2, left, right, origin, goal);
         }
         return result;
      }
   }
   /**
    * Getter for the default abscissa field.
    * @return The assigned default value, which defaults to null.
    */
   T getDefaultValue();
   /**
    * Setter for the default abscissa field.
    * @param defaultValue The intended default value.
    */
   void setDefaultValue(T defaultValue) ;
   /**
    * Getter for the calculationMode field.
    * @return The current calculationMode value.
    */
   CalculationMode getCalculationMode();
   /**
    * Setter for the calculationMode field.
    * @param calculationMode The intended calculationMode value.
    */
   void setCalculationMode(CalculationMode calculationMode);
   /**
    * Locate the {@link SegmentFromReal} which encloses the indicated ordinate.
    * @param ordinate The indicated ordinate.
    * @return The {@link SegmentFromReal} which encloses the indicated ordinate.
    */
   Segment<S, T> locateSegment(S ordinate);
   /**
    * Locate the {@link SegmentFromReal} which encloses the indicated
    * ordinate and return the segment's index.
    * @param ordinate The indicated ordinate.
    * @return The position of the segment enclosing the indicated
    * ordinate.
    */
   int locateSegmentIndex(S ordinate);
   /**
    * Get the number of segments in this contour's collection.
    * @return The size of the segments collection.
    */
   int segmentCount();
   /**
    * Find the segment that encloses the indicated ordinate.  Have
    * that segment interpolate the value at the indicated ordinate.
    * @param ordinate The indicated ordinate.
    * @return The value of the contour at the indicated ordinate.
    */
   T valueAt(S ordinate);
   /**
    * Calculates the area under the contour as an ordinate moves from
    * left to right.
    * @param left The lower ordinate bound.
    * @param right THe upper ordinate bound.
    * @return Area under contour from left to right.
    */
   double areaBetween(S left, S right);
   /**
    * Let y(x) represent the value of the contour at ordinate x.  Then
    * this method calculates the area under the 1/y(x) graph as the
    * ordinate x moves from left to right.  This method is used by
    * the MUSIC-N note-list export to convert relative durations
    * in whole notes to absolute durations in seconds.
    * @param left The lower ordinate bound.
    * @param right THe upper ordinate bound.
    * @return Area under 1/y(x) from left to right.
    */
   double areaBetweenInvert(S left, S right);
   /**
    * Getter for the collection of {@link Segment} instances.
    * @return The list of segments.
    */
   Iterator<Segment<S, T>> iterateSegments();
   /**
    * Add a new segment into the contour, truncating existing segments
    * which would otherwise overlap the new segment.
    * @param left The segment's starting (left) ordinate.
    * @param right The segment's ending (right) ordinate.
    * @param origin The segment's value as-of the left ordinate.
    * @param goal The segment's value as-of the right ordinate.
    * @return The newly created segment.
    */
   Segment<S, T> createSegment(S left, S right, T origin, T goal);
   /**
    * Creates a new {@link Segment} instance.
    * The new segment begins at the indicated starting ordinate and
    * extends to infinity.  The new segment's origin and goal are both
    * the "origin" value provided by the method call.
    * All currently existing segments are truncated wherever
    * they overlap this new segment.
    * @param left The segment starting ordinate.
    * @param origin The segment origin (also its goal).
    * @return The newly created segment.
    */
   Segment<S, T> createOrigin(S left, T origin);
   /**
    * Before doing anything else, calculates the contour value
    * as of the indicated start time.
    * Creates two new {@link Segment} instances.
    * The first segment begins at the indicated start time and
    * extends until the indicated end time.  The first segment's origin
    * is the value calculated above; the goal is the "goal" value provided
    * by the method call.
    * The second segment will begin at the indicated end time and
    * extend to infinity.  The second segment's origin and goal are
    * both the "goal" value provided by the method call.
    * All currently existing segments are truncated if they overlap
    * either of these new segments.
    * @param left The starting ordinate of the transition
    * from origin to goal.
    * @param width The duration of the transition from origin
    * to goal, after which the steady-state segment begins.
    * @param goal The target of the transition (and the constant
    * value held thereafter).
    * @return The newly created {@link Segment} instance.
    */
   Segment<S, T> insertGoal(S left, S width, T goal);
   /**
    * Get the segment at the indicated position.
    * @param position The ordinal position in this contour's collection
    * of segments.
    * @return The segment at the indicated position.
    */
   Segment<S, T> segmentAt(int position);
   /**
    * Get the leftmost segment.
    * @return the leftmost segment.
    */
   Segment<S, T> firstSegment();
   /**
    * Get the rightmost segment.
    * @return the rightmost segment.
    */
   Segment<S, T> lastSegment();
   /**
    * Get the start time of the rightmost segment.
    * @return The start time of the rightmost segment.
    */
   S maxLeft();
   /**
    * Get the end time of the rightmost segment.
    * @return The end time of the rightmost segment.
    */
   S maxRight();
   /**
    * Get the start time of the leftmost segment.
    * @return The start time of the leftmost segment.
    */
   S minLeft();
   /**
    * Get the end time of the leftmost segment.
    * @return The end time of the leftmost segment.
    */
   S minRight();
   /**
    * Copy the segments from the source {@link Contour} instance
    * into this one.
    * @param source The source {@link Contour} instance.
    * @param offset A value to be added to each source ordinate.
    */
   void copySegments(Contour<S, T> source, S offset);
   /**
    * Interface defining a segment of a {@link Contour} collection.
    * @author Charles Ames
    * @param <S> ordinate class (origins and goals)
    * @param <T> Abscissa class (origins and goals)
    */
   interface Segment<S extends Comparable<S>, T extends Comparable<T>> {
      /**
       * Get the entity maintaining a segments collection of which
       * this object is a member.
       * @return The {@link Contour} instance containing this segment.
       */
      Contour<S, T> getContainer();
      /**
       * Get the ordinal position of this segment in its parent
       * {@link Contour} instance's collection of segments.
       * @return The assigned ordinal position of this segment in
       * its parent {@link Contour}
       * instance's collection of segments.
       * Ranges from 1 to size of its parent {@link Contour}
       * segments collection.
       */
      int getPosition();
      /**
       * Get the leftmost ordinate (lower bound).
       * @return The assigned leftmost ordinate, expressed as a
       * double-precision number.
       * @throws UninitializedException when the left ordinate
       * is not initialized.
       */
      S getLeft();
      /**
       * Get the rightmost ordinate (upper bound).
       * @return The assigned rightmost ordinate, expressed as a
       * double-precision number.
       */
      S getRight();
      /**
       * Get the distance from the leftmost ordinate to the
       * rightmost ordinate.
       * @return The distance between the left and right ordinates,
       * expressed using type S.
       * @throws UninitializedException when the leftmost or rightmost
       * ordinate is not initialized.
       */
      S getWidth();
      /**
       * Verify that the indicated ordinate falls within the segment range.
       * @param ordinate The indicated ordinate.
       * @throws IllegalArgumentException when the indicated ordinate falls
       * outside range from leftmost ordinate (inclusive) to rightmost ordinate
       * (exclusive).
       */
      void checkOrdinate(S ordinate);
      /**
       * Get the abscissa when ordinate is leftmost.
       * @return The assigned abscissa when the ordinate is
       * all the way to the left.
       */
      T getOrigin();
      /**
       * Get the contour value when ordinate is rightmost.
       * @return The assigned abscissa when the ordinate is
       * all the way to the right.
       */
      T getGoal();
      /**
       * Interpolate between starting abscissa and ending abscissa, based on
       * the position of the ordinate between leftmost and rightmost.
       * @param ordinate The indicated ordinate.
       * @return The abscissa corresponding to the indicated ordinate.
       */
      T valueAt(S ordinate);
      /**
       * Get the area under the contour between two ordinates
       * @param startOrd The starting ordinate.
       * @param endOrd The ending ordinate.
       * @return The calculated area.
       */
      Double areaBetween(S startOrd, S endOrd);
      /**
       * Get the area under the inverted contour between two ordinates
       * @param startOrd The starting ordinate.
       * @param endOrd The ending ordinate.
       * @return The calculated area.
       */
      Double areaBetweenInvert(S startOrd, S endOrd);
      /**
       * If the present segment continues its predecessor, then merge
       * the two segments.
       * @return A newly created {@link Segment} instance, if the merge
       * happened; otherwise null.
       */
      Segment<S, T> simplify();
   }
}
Listing 1: The Contour interface encapsulates a supporting CalculationMode enumeration and a subsidiary Segment inteface for components.

Interfaces

Up until very recently I had thought that Java interfaces specified methods shared between classes implementing the interface, but nothing else, certainly not code. This impression has been reinforced by statements such as the following from studytonight.com: "When you create an interface it defines what a class can do without saying anything about how the class will do it."

Recently I discovered that the Eclipse IDE accepts active code within interfaces: static variables (not simply constants), static methods, default methods (which I still don't get), and also enumerations. These are interface features which javahelps.com reports to be new with Java 8. Such features make it possible not just to say what methods are available, but to provide code support for such methods. To the extent that these features support range checks and other conformance issues, I think they make a lot of sense.

It also makes sense that enumerations and subsidiary interfaces which affect the internal workings of a primary class be themselves encapsulated within the primary interface declaration. Contours are pieced together from segments. Originally I had one .java file for the Contour and a separate .java file for a ContourSegment interface. By refactoring the child into the parent, I was able to dispense with the "Contour" prefix. When you're working with a Contour, you usually know that any Segment instance belongs to a Contour. In the rare circumstance when you're working with two different Segment classes in the same .java file, you can always qualify this one as Contour.Segment

Generics

The first thing to notice in Listing 1 is that the Contour interface takes two generic parameters:

Both parameters must additionally satisfy the Comparable interface.

My contour package implements two flavors of ordinate. Ordinates often represent time but they don't have to. The Double flavor supports real ordinates like clock time (measured in seconds or milliseconds). The Ratio flavor supports rational ordinates like musical score time (measured in fractions of a whole note). Double is standard Java, but Ratio is homespun. Since my own interest is composing programs, the contour implementations used in my own projects favor Ratio ordinates. However the present treatment of sequence generation is only marginally oriented towards music. For this reason, the current presentation is limited to Double ordinates.

Since this topic area of charlesames.net is directed toward readers interested in sequence generation, the abcissa produced by a contour (in response to an ordinate) will generally be some sort of control parameter guiding the selection of sequence. However, although these contours are wholly adequate for guiding statistical means and deviations, their original purpose was for controlling tempo and dynamics in a musical score-transcription utility.

My contour package favors Double abcissas for one simple reason that in no way prejudges how they are used: Four of the five calculation modes listed above make no sense unless either the abcissa is a double-precision number or the abcissa is a collection whose elements are all double-precision numbers. However there has been the odd exception; in music, for example, a Contour with Pitch abcissas whose calculationMode is DISCRETE. My accomodation has been to develop concrete (instantiatable) classes for Double abcissas but to allow a generic option when abcissas are more exotic.

Enumeration

The second thing to notice in Listing 1 is that the CalculationMode enumeration is internal to Contour and that each element of the enumeration supplies active code implementing its own particular flavor of interpolation.

It makes sense to me that interface components which support functionality that affects the internal workings of contours be themselves internal to the Contour interface declaration.

The purpose of embedding interpolation code directly into CalculationMode items is to avoid in-line switch constructs, dispersed around objects within or even outside the package, each of which switch would require revision whenever a new interpolation mode would be introduced (as happened to me when I added spline flavors). Coding practices which identify potentially deeper problems are identified among software developers as "code smells", and Apiumhub.com lists switch constructs specifically in their "Object-Orientation Abusers" category. By incorporating calculate() methods directly into the enumeration items, the need for a tedious switch construct is replaced within a segment method by a one indirect call: getContour().getCalculationMode().calculate(…).

A criticism of these embedded methods is that they have long parameter lists, which itself is a code smell. The explanation for this is that the methods are not themselves object oriented, and that they require facts that a Segment instance would itself have directly on hand. Supplying a Segment reference in place of the left, right, origin, and goal parameters would have been an alternative solution. That would require an object to implement Contour.Segment in order to make use of these methods. 

/**
 * A {@link ContourBase} maps a generic ordinate (independent variable)
 * to an abscissa (dependent variable) which is generic, but which will
 * often be a double-precision number.
 * The right (upper) ordinate bound of one segment always coincides
 * with the left (lower) ordinate bound of its successor.
 * Contour values are continuous within each segment, but values may
 * change abruptly at segment boundaries.
 * @author Charles Ames
 * @param <S> Ordinate class (left and right ordinates)
 * @param <T> Abscissa class (origins and goals)
 */
public abstract class ContourBase<
S extends Comparable<S>,
T extends Comparable<T>>
extends WriteableEntity implements Contour<S, T> {
   /**
    * A collection of {@link SegmentBase} instances, where the
    * {@link SegmentBase#left} of each successive segment picks up
    * from the {@link SegmentBase#right} of its predecessor.
    */
   private List<SegmentBase<S, T>> segments;
   /**
    * Unmodifiable proxy for {@link segments}, to keep outsiders from
    * modifying segments except through
    * {@link Contour#createSegment(Comparable, Comparable, Comparable, Comparable)}.
    */
   private List<Segment<S, T>> unmodifiableSegments;
   /**
    * Indicates how contour values are calculated in response to
    * ordinates within any particular segment.
    */
   private CalculationMode calculationMode;
   /**
    * Value to be returned by {@link ContourBase#valueAt(double)}
    * when {@link ContourBase#segments} is empty.
    */
   private T defaultValue;
   /**
    * Constructor class for {@link ContourBase} instances with
    * containers.
    * @param container The entity that contains this contour.
    */
   public ContourBase(WriteableEntity container) {
      super(container);
      this.segments = new ArrayList<SegmentBase<S, T> >();
      updateUnmodifiableSegments();
      this.calculationMode = CalculationMode.DISCRETE;
   }
   /**
    * Getter for the {@link ContourBase#defaultValue} field.
    * @return The assigned default value.
    */
   public final T getDefaultValue() {
      return defaultValue;
   }
   /**
    * Setter for the {@link ContourBase#defaultValue} field.
    * @param defaultValue The intended default value.
    */
   public final void setDefaultValue(T defaultValue) {
      this.defaultValue = defaultValue;
   }
   /**
    * Getter for the {@link ContourBase#calculationMode} field.
    * @return The current {@link Contour.CalculationMode} value.
    */
   public final CalculationMode getCalculationMode() {
      return calculationMode;
   }
   /**
    * Minimum ordinate
    * @return The minimum ordinate, as appropriate for the type.
    */
   public abstract S getMinOrdinate();
   /**
    * Maximum ordinate
    * @return The maximum ordinate, as appropriate for the type.
    */
   public abstract S getMaxOrdinate();
   /**
    * Setter for the {@link ContourBase#calculationMode} field.
    * @param calculationMode The intended {@code CalculationMode} value.
    */
   public final void setCalculationMode(CalculationMode calculationMode) {
      if (0 < this.segments.size())
         throw new IllegalArgumentException(
            "Calculation mode may not be changed once segments have been added");
      this.calculationMode = calculationMode;
   }
   /**
    * Locate the {@link SegmentBase} which encloses the
    * indicated ordinate.
    * @param ordinate The indicated ordinate.
    * @return The {@link SegmentBase} which encloses the
    * indicated ordinate.
    */
   public final Segment<S, T> locateSegment(S ordinate) {
      int index = locateSegmentIndex(ordinate);
      if (0 > index) {
         if (null != defaultValue) return null;
         String o = MathMethods.formatDouble(ordinateToDouble(ordinate), 3);
         String o1 = MathMethods.formatDouble(ordinateToDouble(minLeft()), 3);
         String o2 = MathMethods.formatDouble(ordinateToDouble(maxRight()), 3);
         throw new UnsupportedOperationException(
            "Ordinate " + o + " outside range from " + o1 + " to " + o2);
      }
      return unmodifiableSegments.get(index);
   }
   /**
    * Convert an ordinate expressed using the generic
    * type S to a double-precision number.
    * @param ordinate The argument.
    * @return The double-precision result.
    */
   protected abstract double ordinateToDouble(S ordinate);
   /**
    * Confirm that the argument lies within the maximum range
    * for ordinates.
    * @param ordinate The argument.
    * @throws IllegalArgumentException when the argument is null.
    * @throws IllegalArgumentException when the argument falls
    * outside the range from {@link ContourBase#getMinOrdinate()}
    * to {@link ContourBase#getMaxOrdinate()}.
    */
   public void checkOrdinateLimits(S ordinate) {
      if (null == ordinate)
         throw new IllegalArgumentException("Null ordinate");
      if (0 >= getMinOrdinate().compareTo(ordinate)) return;
      if (0 <= getMaxOrdinate().compareTo(ordinate)) return;
      throw new IllegalArgumentException(
         "Invalid ordinate " + ordinate.toString());
   }
   @Override
   public int locateSegmentIndex(S ordinate) {
      checkOrdinateLimits(ordinate);
      if (ordinate.equals(getMaxOrdinate())) return -1;
      int index = segments.size() - 1;
      if (index < 0) return -1;
      Segment<S, T> segment = segments.get(index);
      if (segment.getRight().equals(getMaxOrdinate())) return index;
      return locateSegmentIndex(ordinate, 0, segments.size() - 1);
   }
   /**
    * Recursive helper method which implements segment locating as a binary search.
    * @param ordinate The indicated ordinate.
    * @param left The position of the rightmost segment known whose left bound does not exceed the ordinate.
    * @param right The position of the leftmost segment known whose right bound exceeds the ordinate.
    * @return The position of the segment enclosing the indicated ordinate.
    * @throws RuntimeException when the search fails.
    */
   protected int locateSegmentIndex(S ordinate, int left, int right) {
      if (right < left) return -1;
      int mid = (left + right) / 2;
      Segment<S, T> segment = segments.get(mid);
      if (0 < ordinate.compareTo(segment.getLeft()))
         return locateSegmentIndex(ordinate, left, mid-1);
      if (0 >= ordinate.compareTo(segment.getRight()))
         return locateSegmentIndex(ordinate, mid+1, right);
      return mid;
   }
   @Override
   public int segmentCount() {
      return segments.size();
   }
   @Override
   public final T valueAt(S ordinate) {
      Segment<S, T> segment = locateSegment(ordinate);
      if (null == segment) {
         return defaultValue;
      }
      try {
         T result = segment.valueAt(ordinate);
         return result;
      } catch (Exception e) {
         throw new RuntimeException(e.getMessage(), e);
      }
   }
   @Override
   public double areaBetween(S left, S right) {
      double area = 0;
      S ordinate = left;
      Segment<S, T> segment = locateSegment(ordinate);
      for (;;) {
         S endTime = segment.getRight();
         if (right.compareTo(endTime) <= 0) {
            area += segment.areaBetween(ordinate, right);
            break;
         }
         area += segment.areaBetween(ordinate, endTime);
         ordinate = endTime;
         segment = locateSegment(ordinate);
      }
      return area;
   }
   @Override
   public double areaBetweenInvert(S left, S right) {
      double area = 0;
      S ordinate = left;
      Segment<S, T> segment = locateSegment(ordinate);
      for (;;) {
         S endTime = segment.getRight();
         if (right.compareTo(endTime) <= 0) {
            area += segment.areaBetweenInvert(ordinate, right);
            break;
         }
         area += segment.areaBetweenInvert(ordinate, endTime);
         ordinate = endTime;
         segment = locateSegment(ordinate);
      }
      return area;
   }
   private void updateUnmodifiableSegments() {
      unmodifiableSegments = Collections.unmodifiableList(segments);
   }
   @Override
   public final Iterator<Segment<S, T>> iterateSegments() {
      return unmodifiableSegments.iterator();
   }
   /**
    * Renumber the {@link Segment#position} values so that they
    * proceed sequentially from the indicated starting position
    * rightward.
    * @param startingPosition The indicated starting position.
    */
   protected final void updateIndices(int startingPosition) {
      int limit = segments.size();
      int index = startingPosition;
      SegmentBase<S, T> segment = (SegmentBase<S, T>) segments.get(index);
      if (null == segment) return;
      int i = segments.indexOf(segment);
      segment.setPosition(i++);
      while (++index < limit) {
         segment = (SegmentBase<S, T>) segments.get(index);
         segment.setPosition(i++);
      }
      updateUnmodifiableSegments();
   }
   @Override
   public final Segment<S, T> createSegment(
         S left, S right, T origin, T goal) {
      if (null == left)
         throw new IllegalArgumentException("left is null");
      if (null == right)
         throw new IllegalArgumentException("right is null");
      if (null == origin)
         throw new IllegalArgumentException("origin is null");
      if (null == goal)
         throw new IllegalArgumentException("goal is null");
      if (0 == segments.size()) {
         SegmentBase<S, T> result
            = newSegment(left, right, origin, goal);
         result.setPosition(0);
         segments.add(result);
         updateUnmodifiableSegments();
         return unmodifiableSegments.get(result.getPosition());
      }
      int lastPosition = segments.size() - 1;
      if (left.equals(segments.get(lastPosition).getRight())) {
         SegmentBase<S, T> result
            = newSegment(left, right, origin, goal);
         result.setPosition(lastPosition+1);
         segments.add(result);
         updateUnmodifiableSegments();
         return unmodifiableSegments.get(result.getPosition());
      }
      T existingOrigin;
      {
         int index;
         if (0 == segments.size())
            index = -1;
         else
            index = locateSegmentIndex(left, 0, segments.size() - 1);
         if (0 > index) {
            existingOrigin = getDefaultValue();
         }
         else {
            SegmentBase<S, T> segment
               = (SegmentBase<S, T>) segments.get(index);
            if (left.compareTo(segment.getRight()) < 0) {
               try {
                  existingOrigin = segment.valueAt(left);
               } catch (Exception e) {
                  existingOrigin = getDefaultValue();
               }
            }
            else {
               if (0 == index)
                  existingOrigin = getDefaultValue();
               else {
                  segment = (SegmentBase<S, T>) segments.get(index-1);
                  if (segment.getRight().compareTo(left) < 0) {
                     existingOrigin = getDefaultValue();
                  }
                  else {
                     existingOrigin = segment.getGoal();
                  }
               }
            }
         }
      }
      T existingGoal = valueAt(right);
      for (int position = lastPosition; position >= 0; position--) {
         SegmentBase<S, T> segment = (SegmentBase<S, T>) segments.get(position);
         S existingLeft = segment.getLeft();
         S existingRight = segment.getRight();
         if (position == lastPosition) {
            // gap between existing right and new left - throw exception
            if (existingRight.compareTo(left) < 0) {
               throw new IllegalArgumentException(
                     "Existing right " + existingRight.toString()
                     + " short of new left " + left.toString());
            }
            // existing right coincides with new left - append the segment
            if (existingRight.equals(left)) {
               SegmentBase<S, T> result
                  = newSegment(segment.getRight(), right, origin, goal);
               result.setPosition(lastPosition++);
               segments.add(result);
               updateUnmodifiableSegments();
               return unmodifiableSegments.get(result.getPosition());
            }
         }
         if (existingRight.compareTo(left) < 0) {
            break;
         }
         if (existingLeft.compareTo(right) < 0) {
            if (existingRight.compareTo(left) > 0) {
               if (existingRight.compareTo(right) > 0) {
                  segments.add(position + 1,
                        newSegment(right, existingRight, existingGoal, segment.getGoal()));
               }
               for (;;) {
                  if (existingLeft.compareTo(left) < 0) break;
                  SegmentBase<S, T> oldSegment
                     = (SegmentBase<S, T>) segments.get(position);
                  oldSegment.dispose();
                  segments.remove(position);
                  position--;
                  if (0 > position) {
                     SegmentBase<S, T> result
                        = newSegment(left, right, origin, goal);
                     segments.add(0, result);
                     updateIndices(0);
                     return unmodifiableSegments.get(result.getPosition());
                  }
                  segment = (SegmentBase<S, T>) segments.get(position);
                  existingLeft = segment.getLeft();
                  existingRight = segment.getRight();
               }
               if (existingLeft.compareTo(left) > 0) {
                  segment.setOrigin(origin);
                  segment.setGoal(goal);
                  segment.setLeft(right);
                  updateUnmodifiableSegments();
                  return unmodifiableSegments.get(segment.getPosition());
               }
               SegmentBase<S, T> result
                  = newSegment(left, right, origin, goal);
               segments.add(position+1, result);
               updateIndices(position+1);
               if (segment.getRight().compareTo(left) > 0) {
                  segment.setRight(left);
                  segment.setGoal(existingOrigin);
               }
               updateUnmodifiableSegments();
               return unmodifiableSegments.get(result.getPosition());
            }
         }
      }
      SegmentBase<S, T> result
         = newSegment(left, right, origin, goal);
      result.setPosition(segments.size());
      segments.add(result);
      //System.out.println("<< addValue no overlaps found");
      return result;
   }
   @Override
   public Segment<S, T> createOrigin(S left, T origin) {
      return createSegment(left, getMaxOrdinate(), origin, origin);
   }
   @Override
   public Segment<S, T> segmentAt(int position) {
      return unmodifiableSegments.get(position);
   }
   @Override
   public final Segment<S, T> firstSegment() {
      if (0 == segments.size())
         throw new UnsupportedOperationException("No segments in contour");
      return unmodifiableSegments.get(0);
   }
   @Override
   public final Segment<S, T> lastSegment() {
      if (0 == segments.size())
         throw new UnsupportedOperationException("No segments in contour");
      int index = segments.size() - 1;
      if (0 > index) return null;
      return unmodifiableSegments.get(index);
   }
   @Override
   public final S maxLeft() {
      Segment<S, T> segment = lastSegment();
      return segment.getLeft();
   }
   @Override
   public final S maxRight() {
      Segment<S, T> segment = lastSegment();
      return segment.getRight();
   }
   @Override
   public final S minLeft() {
      Segment<S, T> segment = firstSegment();
      return segment.getLeft();
   }
   @Override
   public final S minRight() {
      Segment<S, T> segment = firstSegment();
      return segment.getRight();
   }
   protected abstract SegmentBase<S, T> newSegment(
         S left, S right, T origin, T goal);
   /**
    * Clear the collection of {@link Contour.Segment} instances.
    */
   public final void clearSegments() {
      for (Segment<S, T> segment : segments) {
         segment.dispose();
      }
      segments.clear();
   }
}
Listing 2: The ContourBase base class. 
/**
 * Base implementation class for a component of a {@link Contour}.
 * @author Charles Ames
 * @param <S> Ordinate class (origins and goals)
 * @param <T> Abscissa class (origins and goals)
 */
public abstract class SegmentBase<
S extends Comparable<S>,
T extends Comparable<T>>
extends WriteableEntity implements Segment<S, T> {
   /**
    * Sequential position of this segment in its parent
    * {@link ContourBase#segments} collection.
    * Ranges from 1 to size of {@link ContourBase#segments}.
    */
   private int position;
   /**
    * Leftmost ordinate (lower bound).
    */
   private S left;
   /**
    * Rightmost ordinate (upper bound).
    */
   private S right;
   /**
    * Calculated distance from {@link SegmentBase#left}
    * to {@link SegmentBase#right}.
    */
   private S width;
   /**
    * Contour value when ordinate equals {@link SegmentBase#left}.
    */
   private T origin;
   /**
    * Contour value when ordinate equals {@link SegmentBase#right}.
    */
   private T goal;
   /**
    * Constructor for {@link SegmentBase} instances
    * @param contour The {@link Contour} which contains this segment.
    */
   public SegmentBase(ContourBase<S, T> contour) {
      super(contour);
      left = null;
      right = null;
      width = null;
      origin = null;
      goal = null;
   }
   /** Set {@link SegmentBase#left}, {@link SegmentBase#right},
    * {@link SegmentBase#origin}, and {@link SegmentBase#goal}
    * for {@link SegmentBase} instance.
    * @param left The leftmost ordinate.
    * @param right The rightmost ordinate.
    * @param origin The abcissa when the ordinate is leftmost.
    * @param goal The abcissa when the ordinate is rightmost.
    */
   public final void setAttributes(S left, S right, T origin, T goal) {
      setLeft(left);
      setRight(right);
      setOrigin(origin);
      setGoal(goal);
   }
   /**
    * Calculate {@link SegmentBase#width} as the distance
    * from {@link SegmentBase#left} to {@link SegmentBase#right}.
    */
   protected abstract void calculateWidth();
   /**
    * Getter for the {@link Entity#container} field.
    * @return The {@link ContourBase} containing this segment.
    */
   @Override
   public ContourBase<S, T> getContainer() {
      @SuppressWarnings("unchecked")
      ContourBase<S, T> container = (ContourBase<S, T>) super.getContainer();
      return container;
   }
   /**
    * Getter for the {@link SegmentBase#position} field.
    * @return The assigned ordinal position of this segment
    * in its parent {@link ContourBase}.
    */
   public int getPosition() {
      return position;
   }
   /**
    * Setter for the {@link SegmentBase#position} field.
    * @param position The intended position of this segment
    * in its parent {@link ContourBase}.
    */
   public final void setPosition(int position) {
      this.position = position;
   }
   /**
    * Getter for the {@link SegmentBase#left} field.
    * @return The assigned leftmost ordinate.
    * @throws UninitializedException when the left
    * ordinate is not initialized.
    */
   public final S getLeft() {
      if (null == left)
         throw new UninitializedException("Left not initialized");
      return left;
   }
   /**
    * Setter for the {@link SegmentBase#left} field.
    * Overrides should always delegate to this.
    * @param left The intended leftmost ordinate.
    */
   protected void setLeft(S left) {
      this.left = left;
      if (null != this.right) calculateWidth();
   }
   /**
    * Getter for the {@link SegmentBase#right} field.
    * @return The assigned rightmost ordinate.
    */
   public final S getRight() {
      if (null == right)
         throw new UninitializedException("Right not initialized");
      return right;
   }
   /**
    * Setter for the {@link SegmentBase#right} field.
    * Overrides should always delegate to this.
    * @param right The intended rightmost ordinate.
    */
   protected void setRight(S right) {
      this.right = right;
      if (null != this.left) calculateWidth();
   }
   /**
    * Getter for the {@link SegmentBase#width} field.
    * @return The distance between the left and right ordinates.
    * @throws UninitializedException when the
    * {@link SegmentBase#width} field is not initialized.
    */
   public final S getWidth() {
      if (null == width)
         throw new UninitializedException("Width not initialized");
      return width;
   }
   /**
    * Setter for the {@link SegmentBase#width} field.  This
    * function should be called by implementations of
    * {@link SegmentBase#calculateWidth()} and nowhere else.
    * @param width The intended distance from left to right.
    */
   protected final void setWidth(S width) {
      this.width = width;
   }
   /**
    * Getter for the {@link SegmentBase#origin} field.
    * @return The assigned segment value when the ordinate is
    * all the way to the left.
    * @throws UninitializedException when the {@link SegmentBase#origin}
    * field is not initialized.
    */
   public final T getOrigin() {
      if (null == origin)
         throw new UninitializedException("Origin not initialized");
      return origin;
   }
   /**
    * Setter for the {@link SegmentBase#origin} field.
    * @param origin The intended segment value when the
    * ordinate is all the way to the left.
    */
   protected void setOrigin(T origin) {
      this.origin = origin;
   }
   @Override
   public T getGoal() {
      if (null == right)
         throw new UninitializedException("Right not initialized");
      return goal;
   }
   /**
    * Setter for the {@link SegmentBase#goal} field.
    * @param goal The intended segment value when the
    * ordinate is all the way to the right.
    */
   protected void setGoal(T goal) {
      this.goal = goal;
   }
   @Override
   public Double areaBetween(S startOrd, S endOrd) {
      throw new IllegalArgumentException("Method not implemented");
   }
   @Override
   public Double areaBetweenInvert(S startOrd, S endOrd) {
      throw new IllegalArgumentException("Method not implemented");
   }
}
Listing 3: The SegmentBase base class. 
/**
 * The {@link ContourFromReal} class refines {@link ContourBase} for
 * double-precision ordinates.  Abscissas remain generic.
 * An example of a double-precision ordinate is time, measured in
 * seconds.
 * @author Charles Ames
 * @param <T> Range class (origins and goals)
 */
public abstract class ContourFromReal<T extends Comparable<T>>
extends ContourBase<Double, T> implements Contour<Double, T> {
   /**
    * Minimum ordinate
    */
   public static final double MIN_ORDINATE = Integer.MIN_VALUE;
   /**
    * Maximum ordinate
    */
   public static final double MAX_ORDINATE = Integer.MAX_VALUE;
   /**
    * Constructor class for {@link ContourFromReal} instances with containers.
    * @param container The entity that contains this contour.
    */
   public ContourFromReal(WriteableEntity container) {
      super(container);
   }
   /**
    * Constructor class for {@link ContourFromReal} instances without containers.
    */
   public ContourFromReal() {
      this(null);
   }
   @Override
   public final Segment<Double, T> insertGoal(Double left, Double width, T goal) {
      Double right = left + width;
      Segment<Double, T> result = createSegment(left, right, valueAt(left), goal);
      Double maxOrdinate = getMaxOrdinate();
      if (maxOrdinate > right) {
         result = createSegment(right, maxOrdinate, goal, goal);
      }
      return result;
   }
   @Override
   public void copySegments(Contour<Double, T> source, Double offset) {
      setCalculationMode(source.getCalculationMode());
      Iterator<Segment<Double, T>> iterator = source.iterateSegments();
      while (iterator.hasNext()) {
         Segment<Double, T> segment = iterator.next();
         createSegment(offset + segment.getLeft(), offset + segment.getRight(),
               segment.getOrigin(), segment.getGoal());
      }
   }
   @Override
   public Double getMinOrdinate() {
      return MIN_ORDINATE;
   }
   @Override
   public Double getMaxOrdinate() {
      return MAX_ORDINATE;
   }
   @Override
   protected double ordinateToDouble(Double ordinate) {
      return ordinate;
   }
}
Listing 4: The ContourFromReal base class.

Implementation

The implementation classes for my contour package have two parallel type hierarchies with increasingly specific subclasses:

There are corresponding second- and third-tier implementation classes for Ratio ordinates: The second-tier classes are ContourFromRational<T>, and RationalSegment<T>. The third-tier classes are ContourFromRealFromRatio and ContinuousRationalSegment. These rational classes are outside the scope of the current presentation, so listings are not provided.

The first-tier pairing of ContourBase and SegmentBase does as much as possible simply knowing that contour ordinals implement Comparable.

The heart of the data model is the ContourBase.segments collection, whose elements are Segment instances. As stated previously, package consumers are expected to manage the contents of this collection using Contour.createSegment(), which takes care that the train of segments remains well formed. That means that while consumers should be free to examine segment details, they should be able neither to delete segments from the collection nor to insert new segments which were externally instantiated. Neither should consumers be able directly to alter any segment properties.

The first-tier classes enforce isolation of segments and its contents in several ways. First, the segments collection itself is strictly private. Queries of its content are handled through an UnmodifiableList, which acts as a proxy. It is not clear to me that the elements of an UnmodifiableList are themselves unmodifiable. However, only getters are exposed for the five SegmentBase properties: left, right, origin, goal, and position. The setters are held close as protected methods which can only be seen either by objects in the same package or by direct subclasses. 

/**
 * The {@link SegmentFromReal} class implements a segment of a {@link ContourFromReal}
 * collection.  It refines {@link SegmentBase} for double-precision ordinates.
 * Abscissas remain generic.
 * @author Charles Ames
 * @param <T> Abscissa class (origins and goals)
 */
public abstract class SegmentFromReal<T extends Comparable<T>>
extends SegmentBase<Double, T> {
   /**
    * Constructor for {@link SegmentFromReal} instances
    * @param contour The {@link ContourFromReal} which contains this segment.
    */
   public SegmentFromReal(ContourFromReal<T> contour) {
      super(contour);
   }
   /** Constructor for {@link SegmentFromReal} instances
    * @param contour The {@link ContourFromReal} which contains this segment.
    * @param left The minimum ordinate (inclusive).
    * @param right The maximum ordinate (exclusive).
    * @param origin The segment value at the left ordinate.
    * @param goal The segment value at the right ordinate.
    * @throws IllegalArgumentException when the right ordinate
    * is not appreciably greater than the left ordinate.
    */
   public SegmentFromReal(ContourFromReal<T> contour,
         double left, double right, T origin, T goal) {
      super(contour);
      setAttributes(left, right, origin, goal);
   }
   @Override
   public void wipe() {
      super.wipe();
   }
   /**
    * Calculate {@link SegmentFromReal#width} as the distance from
    * {@link SegmentFromReal#left} to {@link SegmentFromReal#right}.
    */
   protected final void calculateWidth()
   {
      Double left = getLeft();
      Double right = getRight();
      Double width;
      ContourFromReal<T> contour = getContainer();
      if (left <= contour.getMinOrdinate())
         width = contour.getMaxOrdinate();
      else if (right >= contour.getMaxOrdinate())
         width = contour.getMaxOrdinate();
      else
         width = right - left;
      if (width < MathMethods.TINY) {
         throw new IllegalArgumentException("Segment right "
               + MathMethods.formatDouble(right, 3)
               + " not appreciably greater than segment left "
               + MathMethods.formatDouble(left, 3));
      }
      setWidth(width);
   }
   /**
    * Getter for the {@link Entity#container} field.
    * @return The {@link ContourFromReal} containing this segment.
    */
   @Override
   public ContourFromReal<T> getContainer() {
      ContourFromReal<T> container = (ContourFromReal<T>) super.getContainer();
      return container;
   }
   @Override
   public final void checkOrdinate(Double ordinate) {
      if (getLeft() > ordinate || ordinate > getRight()) {
         throw new IllegalArgumentException("Ordinate [" + ordinate
               + "] out of range from "
               + MathMethods.formatDouble(getLeft(), 4)
               + " to " + MathMethods.formatDouble(getRight(), 4));
      }
   }
   @Override
   public T valueAt(Double ordinate)  {
      if (ordinate < getLeft() || ordinate > getRight())
         throw new IllegalArgumentException("Ordinate [" + ordinate + "] outside range from "
               + MathMethods.formatDouble(getLeft(), 4)
               + " to " + MathMethods.formatDouble(getRight(), 4));
      return getOrigin();
   }
   @Override
   public SegmentFromReal<T> simplify() {
      ContourFromReal<T> contour = (ContourFromReal<T>) getContainer();
      int position = getPosition();
      if (0 == position) return null;
      SegmentFromReal<T> predecessor = (SegmentFromReal<T>) contour.segmentAt(position-1);
      if (null == predecessor) return null;
      double left = predecessor.getLeft();
      double right = getRight();
      try {
         double predecessorOrigin = (double) predecessor.getOrigin();
         double predecessorGoal = (double) predecessor.getGoal();
         double currentOrigin = (double) getOrigin();
         double currentGoal = (double) getGoal();
         double value = contour.getCalculationMode().calculate(getLeft(),
               left, right-left, predecessorOrigin, currentGoal);
         if (!MathMethods.haveSmallDifference(value, predecessorGoal)
               || !MathMethods.haveSmallDifference(value, currentOrigin)) return null;
         return (SegmentFromReal<T>) contour.createSegment(
               left, right, predecessor.getOrigin(), getGoal());
      }
      catch (ClassCastException e) {
         T predecessorOrigin = predecessor.getOrigin();
         T predecessorGoal = predecessor.getGoal();
         T currentOrigin = getOrigin();
         T currentGoal = getGoal();
         if (0 != predecessorOrigin.compareTo(predecessorGoal))
            throw new UnsupportedOperationException(getClass().getSimpleName()
                  + " not equipped to simplify non-discrete segments except scalar double");
         if (0 != currentOrigin.compareTo(currentGoal))
            throw new UnsupportedOperationException(getClass().getSimpleName()
                  + " not equipped to simplify non-discrete segments except scalar double");
         if (0 != currentOrigin.compareTo(predecessorGoal)) return null;
         return (SegmentFromReal<T>) contour.createSegment(
               left, right, predecessorOrigin, currentGoal);
      }
   }
}
Listing 5: The SegmentFromReal base class.

The second-tier pairing of ContourFromReal and SegmentFromReal supply the additions and subtractions that have to be coded separately (from ContourFromRational and RationalSegment). Because Java's Double class participates in no interface supporting arithmetic methods like add() or subtract(), and because it's sensible programming not to replicate logic in two places (particularly something as complex as ContourBase.createSegment(), I've had to institute workarounds for direct ordinate operations.

These are the workarounds which ContourBase delegates out to ContourFromReal and ContourFromRational: 

/**
 * A {@link RealContourFromReal} maps double-precision ordinates (independent variable)
 * to abscissas (dependent variable) are also double-precision numbers.
 * The right (upper) ordinate bound of one segment always coincides with the left (lower) ordinate bound
 * of its successor.
 * An example of a double-precision ordinate is time, measured in seconds.
 * Contour values are continuous within each segment, but values may change abruptly at segment boundaries.
 * @author Charles Ames
 */
public class RealContourFromReal extends ContourFromReal<Double> {
   @Override
   protected RealSegmentFromReal newSegment(Double left,
         Double right, Double origin, Double goal) {
      return new RealSegmentFromReal(this, left, right, origin, goal);
   }
}
Listing 6: The RealContourFromReal implementation class. 
/**
 * A {@link RealSegmentFromReal} class implements a segment of a
 * {@link RealContourFromReal} collection.  It refines {@link ContourFromReal}, which
 * already has double-precision ordinates, to have double-precision abscissas as
 * well.
 * @author Charles Ames
 */
public class RealSegmentFromReal extends SegmentFromReal<Double> {
   /** Constructor for {@link RealSegmentFromReal} instances
    * @param contour The {@link RealContourFromReal} which
    * contains this segment.
    * @param left The minimum ordinate (inclusive).
    * @param right The maximum ordinate (exclusive).
    * @param origin The segment value at the left ordinate.
    * @param goal The segment value at the right ordinate.
    * @throws IllegalArgumentException when the right ordinate
    * is not appreciably greater than the left ordinate.
    */
   public RealSegmentFromReal(ContourFromReal<Double> contour,
         double left, double right, double origin, double goal) {
      super(contour, left, right, origin, goal);
   }
   @Override
   public final Double valueAt(Double ordinate) {
      return getContainer().getCalculationMode().calculate(
            ordinate,
            getLeft(), getRight(), getOrigin(), getGoal());
   }
   @Override
   public final Double areaBetween(Double startOrd, Double endOrd)  {
      return getContainer().getCalculationMode().areaBetween(
            startOrd, endOrd,
            getLeft(), getRight(), getOrigin(), getGoal());
   }
   @Override
   public Double areaBetweenInvert(Double startOrd, Double endOrd) {
      return getContainer().getCalculationMode().areaBetweenInvert(
            startOrd, endOrd,
            getLeft(), getRight(), getOrigin(), getGoal());
   }
}
Listing 7: The RealSegmentFromReal implementation class.

The third-tier pairing of RealContourFromReal and RealSegmentFromReal fills in the few remaining details necessary to produce concrete, non-abstract, and instantiatable implementations.

The abstract ContourBase class specifies a newSegment() method without providing a body. Implementing this method is left to the concrete (instantiatable) subclasses, since this the Contour() header which knows which class of Segment() detail is appropriate. And as Listing 6 confirms, this is the only procedural detail needed from the concrete RealContourFromReal() implementation class.

The Segment interface specifies valueAt(), areaBetween(), and areaBetweenInvert() methods. The enumerated CalculationMode options provide helper methods, but these all limit ordinates and abcissas to double-precision arguments. Now RealSegmentFromReal is a concrete (instantiatable) implementation of Segment(), and both the ordinates and the abcissas of this RealSegmentFromReal satisfy these helper-function requirements. The only procedural details needed from RealSegmentFromReal are class methods which plug their arguments into the CalculationMode helper methods. That's precisely what happens in Listing 7.

Alternatively, the abcissa type might be some aggregation (e.g. an array or List) whose elements are double numbers. The density to timbre-weight mappings of Xenakis's Stochastic Music Program give an example of this. In Xenakis's program, the independent variable is the section density, which ranges continuously along a logarithmic scale from 0 to 6. The data provided to the program consisted primarily of seven arrays. The first array held timbre likelihoods for section density 0. The second array held timbre likelihoods for section density 1, and so forth. Thus if for a given section, the sequence generator responsible for section densities produced a value of 3.7, then the Stochastic Music Program would derive a momentary array whose scope applies strictly to the current section. The likelihood associated by this momentary array with timbre k would be calculated by interpolating between the kth element of the data array for section density 3 and the kth element of the data array for section density 4. The interpolation factor would be 0.7.

The density to timbre-weight scenario just described is effectively a statistical distribution with parametric control. The range of the distribution is discrete, extending as it does over the list of timbres (read: instruments played a certain way) glean by Xenakis from his ensemble. It could be implemented as an array of RealContourFromReal instances, once for each timbre. That would would allow more fluid data entry. If one wanted to keep the structure of specifying a complete timbre-likelihood array for each integral section density, then a custom Contour/Segment pair could be developed whose ordinates were Double arrays. The Segment/valueAt() would need to apply CalculationMode/valueAt() element-by-element, and some discipline should be imposed to prevent inconsistent array dimensions. None of that is a heavy lift.

Comments

  1. The term “equal ratios curve” was coined by John Rogers and John Rockstroh in a paper entitled “Score-Time and Real-Time” given at the 1978 International Computer Music Conference.

© Charles Ames Page created: 2022-08-29 Last updated: 2022-08-29