Demonstration 10
Comparative Search

Introduction

Demonstration 10 provides the practical component for Chapter 12: “Comparative Search” of my unpublished textbook on composing programs. It illustrates how comparative searches can be used to compose a piece of music, and in doing so, illustrates the principle of bottom-up design. The technique here called “comparative search”¹ comes directly from Artificial Intelligence, where it is known as “alpha-beta pruning”.

As contrasted with the top-down deductive approach used to generate Demonstration 8 and Demonstration 9, the form of Demonstration 10 is induced from the bottom up, on the basis of qualities inherent in pre-composed material. The approach reflects the author's composition Protocol to the extent that Demonstration 10's material consists of recurrent modules, each comprised of several chords, and to the extent also that the order of progression is contextually determined. Like Demonstration 7, Demonstration 10 employs arpeggiation to adapt this chordal material to the monophonic nature of the clarinet.

Compositional Directives

The process of composing Demonstration 10 divides into three stages of production:

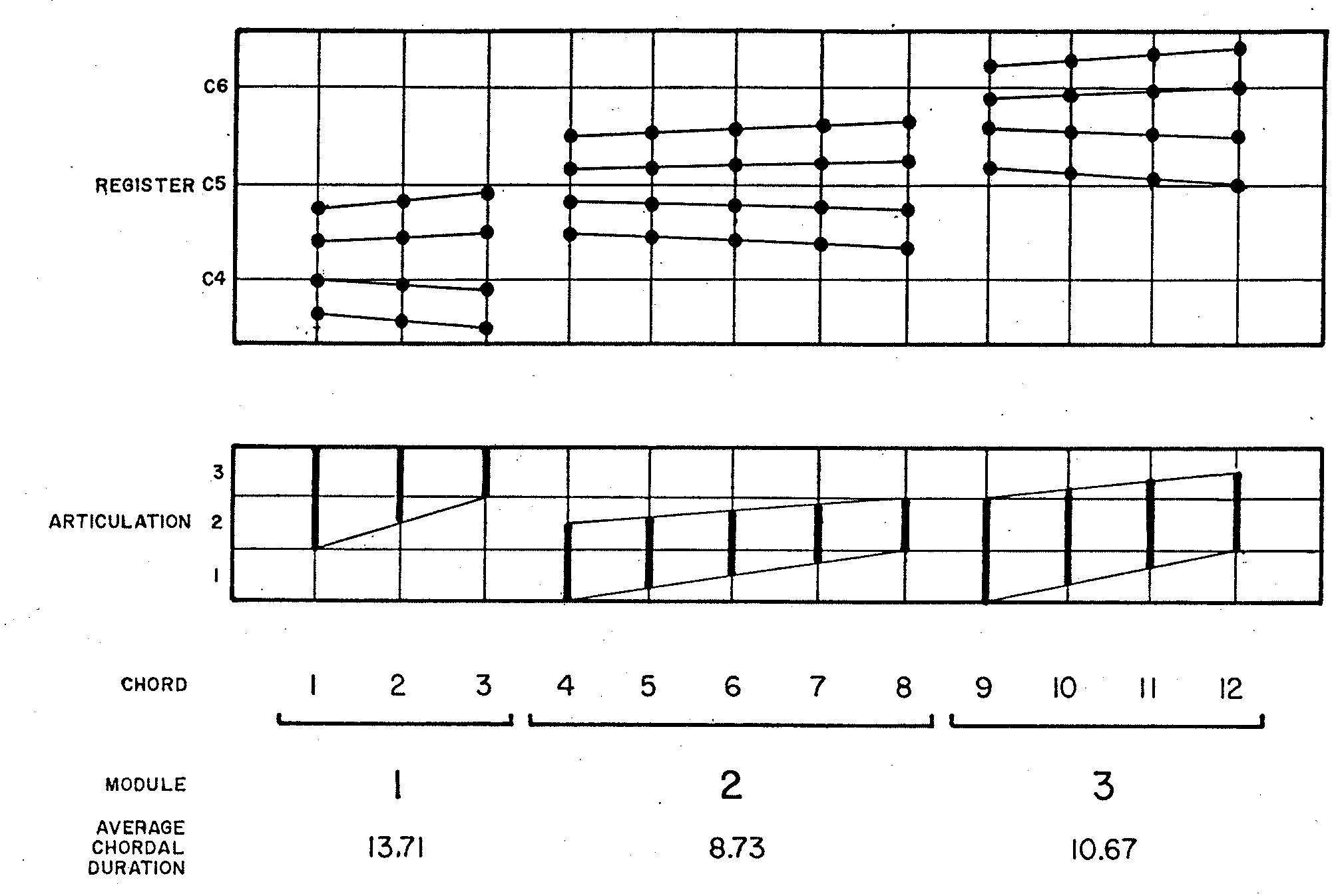
• Stage I: Material — This stage takes the registral information shown in Figure 1 and composes the 12 chords shown in Figure 2.
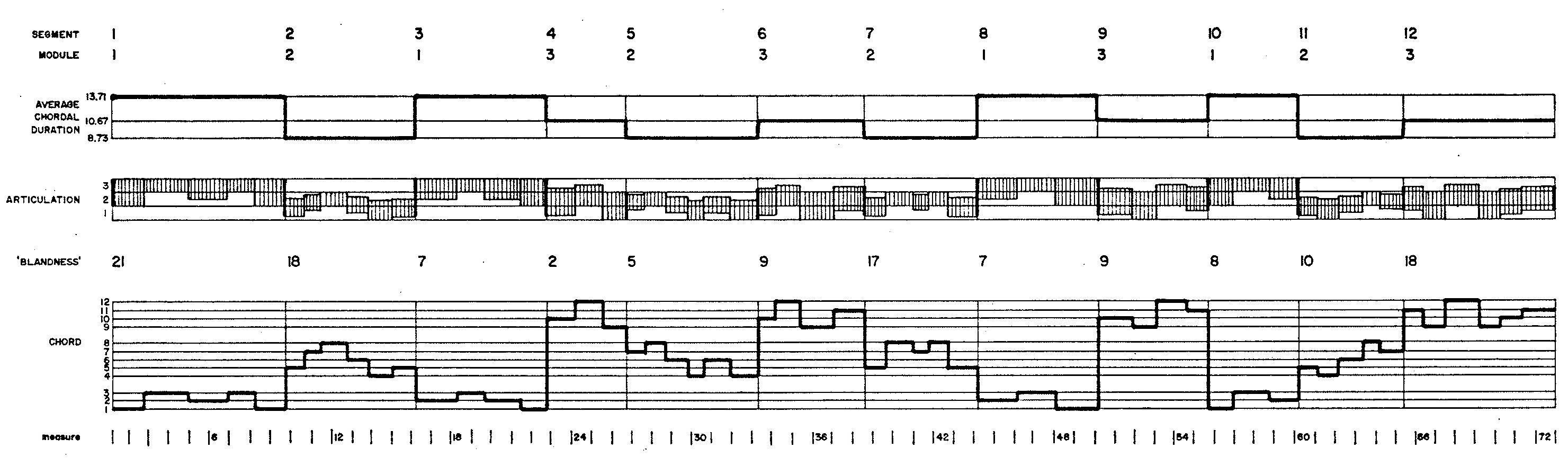
• Stage II: Form — This stage steps through each of the segments described in Table 1 and arranges the segment's chords into the progression detailed in Figure 3.
• Stage III: Content — The third stage iterates through the chord progression detailed in Figure 3 using with the ranges of articulation listed in Figure 1 to arpeggiate the chords in a manner playable on the clarinet.

Material

Figure 1 shows how the material for Demonstration 10 is organized. The material will consist of twelve chords grouped into three modules. Each module is described by a characteristic register, by a range of articulations, and by an average chordal duration. Dots on the registral graphs indicate center pitches of a five-semitone gamut. The bold vertical lines on the graph of articulations define regions of relative likelihood for three styles of playing: (1) slurred, (2) normal, and (3) detached. The average chordal duration supplied for each module indicates sixteenth notes.

Stage I of the composing process seeks to reconcile directives intended to promote chromatic diversity, dissonance, and divergent part-leading. The most emphatic of these directives assume the status of constraints:

1. As a minimum condition of chromatic diversity, no two chords may share more than two degrees of the chromatic scale.
2. As a minimum condition of dissonance, no two pitches in a chord may occupy the same degree of the chromatic scale.
3. Parallelisms are restricted in the following way:
   • For any pair of chords residing in the same module, the interval relating any two parts in one chord may not be duplicated in the corresponding two parts of the other chord.
   • For any pair of chords residing in different modules, the intervals relating any three parts in one chord may not be duplicated in the corresponding three parts of the other chord.

These constraints, along with the heuristic criteria described below, are formulated with the specific rhetoric of Demonstration 10 in mind. The purpose here is in no way to promote stylistic principles, but rather to illustrate how assertions of this kind can be implemented programmatically.

Each chord will be composed using a comparative search; backtracking is limited to the extent that once the program advances to a new chord, no revision of any previous chord may happen. Subject to the constraints listed above, each search employs two criteria for evaluating candidate chords.

• Chromatic redundancy — For each degree in a chord, the program tallies how many ties the degree appears in previously composed chords. The maximum of these tallies yields a worst-case measure of the chord's chromatic redundancy.
• Sonorous quality — The program derives this number by first tallying the number of times each type of interval occurs in a chord and then packing these tallies into a single number which assigns greater significance to more consonant intervals.

Understand that a comparative search prunes fruitless solution paths whenever it deems the current partial candidate less satisfactory than any complete solution already discovered. This feature requires criteria to be expressed in a contrary way, as practices to avoid rather than practices to encourage. Thus the present search seeks to discourage redundancy rather than encourage diversity; likewise it seeks to discourage consonances rather than encourage dissonances. The prioritization of criteria works out as follows: less chromatically redundant candidates displace incumbents; more redundant candidates are discarded. When a candidate and an incumbent have equal chromatic redundancy, then the candidate displaces the incumbent only when the candidate has fewer consonances.

Figure 2 shows the results of the twelve chordal searches. The two key values supplied beneath each chord indicate (1) chromatic redundancy relative to the proceeding chords and (2) sonorous quality expressed as packed tallies of intervallic types, with the greater significances associated with the more consonant intervals. Notice that the formulation of ‘sonorous quality’ favors chords of the diminished seventh (chords 2 and 4) over chords of superimposed fourths, fifths, and tritones (especially chord 8, but see also chords 7 and 11).

With 5 pitches available to each part and 4 parts, the theoretic total of candidate chords for each search is 5⁴=625. In practice, the constraints against doublings, parallelism, and chromatic overlap substantially reduce the number of acceptable chords. Only when a partial chord meets the absolute requirements imposed by these constraints does a search proceed to evaluate its chromatic redundancy and sonorous quality.

Form

Demonstration 10 divides into twelve segments, each of which draws material from a single module. Table 1 lists segment attributes. The number of chords appearing in a segment depend both upon the length of the segment and upon the module's average chordal duration.

Segment	Measure & Beat	Duration	Module	Chordal Positions	Chords												Possible Arrangements
					1	2	3	4	5	6	7	8	0	10	11	12
1	1:0	69	1	5	XX	X	XX										120
2	9:5	52	2	6				X	XX	X	X	X					720
3	16:1	52	1	4	X	XX	X										24
4	22:5	25	3	3									X	X		X	6
5	26:5	53	2	6				XX		XX	X	X					720
6	33:2	42	3	4									X	X	X	X	24
7	38:4	45	2	5					XX		X	XX					120
8	44:1	48	1	3	X	X	X										6
9	50:1	45	3	4									X	X	X	X	24
10	55:6	35	1	3	X	X	X										6
11	60:1	42	2	5				X	X	X	X	X					120
12	65:3	61	3	6									XX	X	XX	X	720

Table 1: Segment attributes for Demonstration 10

The column labeled “Possible Arrangements” gives numbers calculated as N factorial, where N is comes from the column labeled “Chordal Positions”. Since N factorial counts how many ways N different items can be arranged, this number is overestimates arrangements. However the purpose in supplying this number was to verify that the search space space will be reasonable for a comparative search, and that purpose is adequately served.

The chordal content of each segment was itself derived programmatically. Notice that Table 1 allocates a total of 5+4+3+3=15 positions for module 1, 6+6+5+5=22 positions for module 2, and 3+4+4+6=17 positions for module 3. With these position counts it was not possible to represent every chord an equal number of times, yet the chord counts are close to uniform: 5+5+5=15 for module 1, 4+5+4+4+5=22 for module 2, and 5+4+4+4=17 for module 3. Which chords went with which segment was determined by random shuffling.

Given the chordal content of a segment, Stage II of the composing process is responsible for determining in what order the chords will occur. This problem is fundamentally one of organizing a statistical frame; where programs for earlier Demonstrations would have either shuffled the chords randomly (Demonstration 3) or sorted the chords so that preferred chords would be placed in the most desirable positions (Demonstration 7), the technique of comparative search sensitizes the current program to context when it considers alternate chordal progressions.

By contrast to the chord-composing searches described above, the searches for ‘optimal’ chordal progressions impose no constraints. The heuristic criteria are once again expressed in a contrary way so that minimax comparisons can be used to prune unfruitful search paths. There are two of these criteria:

• Blandness — For each progression of chords, the program tallies how many pairs of consecutive chords share 0, 1, 2, or 4 chromatic degrees in common. It then packs these tallies into a single key, assigning greater significances to consecutive chords sharing more degrees. The resulting quantity gives a measure of ‘blandness’ in the progression, and the search seeks to minimize this quantity in the worst cases.
• Imbalance — In order to keep the chordal resources in balance, the program maintains cumulative statistics reflecting the total duration over which each chord has been employed. The imbalance of a progression is a vector determined by considering the largest statistic as a primary element, the next largest statistic as a secondary element, and so on for each statistic.

The goal of the search is to arrange the chords in such a manner that blandness will be minimal. Given progressions of equal blandness, a subsidiary goal is to arrange the chords so as to assign longer durations to those chords which occur least often in a segment. Random shuffling insures unbiased selection between progressions which the program otherwise judges equally suitable.

The result of the search appears in Figure 3. Modules and chord numbers refer back to Figure 1 and Figure 2. The blandness given for each segment reflects pairs of consecutive chords sharing one or more common chromatic degrees.

The transcribed product appears in Figure 4.

Implementation

The following explanations seek to illustrate comparative searches in play. The explanations are peppered with line numbers, but you are are by no means expected to chase down every line of code. Rather, you should follow through with line numbers only when you have a specific question that the narrative is not answering.

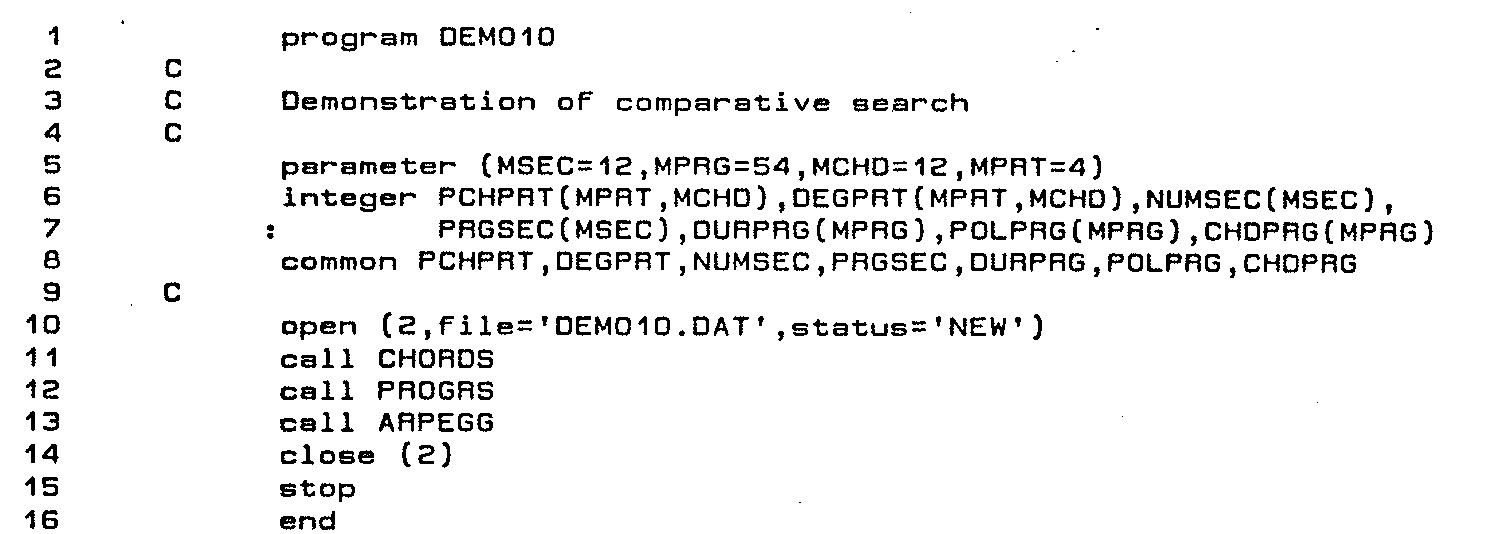
Program DEMO10 proper appears as Listing 1; the BLOCK DATA routine used to initialize COMMON memory variables appears as Listing 2. The body of program DEMO10 simply calls out to three subroutines, each of which implements a stage of production. The call to subroutine CHORDS in line 11 invokes Stage I, which generates the chordal material. The call to subroutine PROGRS in line 12 invokes Stage II, which fleshes out the mid-level form by determining which chord should follow which. The call to subroutine ARPEG

Listing 1: Program DEMO10, lines 1-60.		Listing 2: BLOCK DATA routine for program DEMO10.

Since several items of information are necessary to describe each option selected by a decision, these items are organized into parallel stacks accessed by a single index.

The symbols shared between program DEMO10 and its subroutines adhere to five root abbreviations pertaining to the various categories of information in the musical design:

• The abbreviation CHD signifies information pertaining to entire chords. The parameter MCHD gives the total number of chords in Figure 1, while the variable ICHD indicates one specific chord at a time. In subroutine CHORDS, array element MODCHD(I) indicates which module contains the Ith chord.
• The abbreviation PRT signifies information pertaining to individual parts within a chord. The parameter MPRT gives the number of parts per chord in Figure 1, while the recursive index IPRT indicates one specific part within one specific chord. Array element PCHPRT(I,J) gives the pitch selected by CHORDS for the Ith part of the Jth chord, while the element DEGPRT(I,J) gives the corresponding chromatic degree.
• The abbreviation SEG signifies information pertaining to individual segments. The parameter MSEG gives the total count of segments in Table 1, while the variable ISEG indicates the segment currently being composed. Array element NUMSEG(I) gives the number of chordal positions from column 5 of Table 1; array element PRGSEG(I) indicates the first position in the progression occurring in the Ith segment.
• The abbreviation PRG signifies information pertaining to the progression of chords. The parameter MPRG gives the total number number of chords in all segments combined, which is the sum of column 5 of Table 1. The recursive index IPRG indicates specific positions in the progression. Array element DURPRG(I) gives the duration allotted to the Ith position; array element CHDPRG(I) indicates which of the 12 chords has been selected by subroutine PROGRS for this position.
• Array POLPRG contains pools of chords to be used in each segment.

Chords

Subroutine CHORDS is listed in Listing 3 (a) and Listing 3 (b). This subroutine implements Stage I of compositional processing, which selects pitches for chords. It uses raw material from array REGPRT to populate chordal content into arrays PCHPRT and DEGPRT.

Listing 3 (a): Subroutine CHORDS, lines 1-60.		Listing 3 (b): Subroutine CHORDS, lines 61-117.

The outermost loop of subroutine CHORDS (lines 18-115) iterates on the variable ICHD, so as to initiate comparative searches for each of the 12 chords.

The next-to-outermost loop (lines 23-114) implements the recursive mechanism for each search. The level of recursion is tracked by the part index IPRT, which advances and retreats in the time dimension. The variable IDX gives

The heart of the chord-generating process is the recursive mechanism implemented as the next-to-outermost loop from line 23 to line 114. Like the recursive implementations for Demonstration 8 Demonstration 9, the loop indexing here is bi-directional:

• Variable IPRT iterates forward and back from low register to high register, where IPRT=1 is the lowest register in the chord.
• Variable IPRG iterates from 1 to MPCH and tracks the option under consideration for the current part. Each change in IPRT disrupts the forward progression of IDX; therefore, array IDXPRT keeps track of IDX for various IPRT values. Thus whenever the recursive loop advances to the next part, it pushes the value of IDX into IDXPRT(IPRT) (line 28). Conversely when the recursive loop retreats to the previous part, it pops the value of IDX from IDXPRT(IPRT) (line 26).

Each loop iteration begins first by advancing IDX one position to the right (line 26), then immediately testing (line 27) whether IDX has reached its limit. The process advances to the next (higher) part in line 98 and immediately thereafter initializes IDXPRT(IPRT) to 0. COMPOS retreats to the previous (lower) part in line 105, but the value of IDX is not reclaimed until the loop iterates (line 26).

Options for parts in the chordal search combine the registral locus stored in array element REGPRT(IPRT,ICHD) (initialized in lines 14-17) along with displacements stored in array element OFFSET(IPRT). These displacements range from 0 to 2 semitones above and below the locus (line 11). From the locus and displacement, CHORDS computes a pitch (line 29) and a degree (line 32). Arrays PCHTMP and DEGTMP store these values temporarily until such tie as CHORDS determines whether the current candidate compares favorably or not to the incumbent. In the former case, CHORDS transfers values from PCHTMPand DEGTMP to more permanent residence in PCHPART and DEGPRT, at least until a better chord is encountered.

The first thing CHORDS does when considering an option is to check for doublings (lines 33-35), parallelism (lines 39043 along with the logical function PARALL listed in Listing 4) and chromatic overlap (lines 46-47). Only when these constraints are satisfied does CHORDS attempt any heuristic evaluation.

Evaluation of chromatic redundancy employs arrays USEDEG and USETMP. Array element USEDEG(I) tallies the number of already-composed chords employing the Ith degree of the chromatic scale, while array element USETMP(J) holds the largest of these tallies for the first J degrees in the candidate. CHORDS evaluates the chromatic redundancy of each partial candidate (lines s61-66) by selecting the maximum between the current degree's tally and largest value for all previous parts; the variable LUSE gives the chromatic redundancy of the incumbent.

Evaluation of sonorous quality proceeds only when the candidate is no more redundant than the incumbent. Array QALTVL (initialized in line 12) indicates the relative significances for each type of interval from the semitone to the major seventh. CHORDS considers only intervals between degrees, without regard to inversion or octave displacement (lines 77-79). Since four-part chords are characterized by 6 intervals, significances in QALTVL are expressed as powers of 7. Array element QUALTMP(I) gives the contributions to the candidate of all intervals resulting from the first I degrees, while the variable LAQAL gives the sonorous quality of the incumbent.

Chordal Progression

Subroutine PROGRS is listed in Listing 5 (a) and Listing 5 (b). This subroutine implements Stage II of compositional processing, which arranges chords within segments. It uses raw material from array POLPRG along with processed material populated into arrays PCHPRT and DEGPRT by subroutine CHORDS. Subroutine PROGRS in turn populates chordal content into arrays PCHPRT and DEGPRT.

Listing 5 (a): Subroutine PROGRS, lines 1-60.		Listing 5 (b): Subroutine PROGRS, lines 61-113.

PROGRS's main loop (lines 31-116) iterates on the variable ISEG, so as to initiate comparative searches for each of the 12 segments listed in Table 1.

PROGRS draws its raw material from array POLPRG The contents of this array follow Table 1 and are initialized in line 13 of the BLOCK DATA routine. Chords are listed in the following way: for the Ith segment of the piece, set IPRG=PRGSEG(I) and NUM=NUMSEG(I); the array elements POLCHD(IPRG) through POLCHD(IPRG+NUM-1) hold the appropriate pool of chords.

The heart of the chord-arranging process is the recursive mechanism implemented as the next-to-outermost loop from line 41 to line 115 The loop indexing is bi-directional:

• The segment-local variable ITMP iterates forward and back through the current segment's chordal positions, where ITMP=1 is the segment's leftmost position. ITMP ranges from 1 to NUMSEG(ISEG). The variable LPRG indicates the position globally. It ranges from LPRG1=PRGSEG(ISEG) up to LPRG2=PRGSEG(ISEG)+NUMSEG(ISEG)-1.
• Array element PRGTMP(ITMP) gives the index to the option under consideration for position ITMP. In this case, options are drawn with regard to order but without replacement from the pool of chords stored in array elements POLPRG(LPRG1) through POLPRG(LPRG2).

Array CHDTMP(ITMP) stores POLPRG(PRGTMP(ITMP)) temporarily until such time as PROGRS determines whether the candidate progression compares favorably or not to the incumbent. If so, CHDTMP's content is transferred to more permanent residence in CHDPRG, at least until a better progression is encountered.

Prior to its first search PROGRS analyzes each pair of chords for common chromatic degrees (lines 14-28). Upon completion of this analysis, array element BLNCHD(I,J) gives the number of degrees shared in common by the Ith and Jth chords. We shall take this number as reflecting the relative blandness of progressing directly from chord I to chord J. In deriving compound blandnesses for progressions of several chords, PROGRS assigns greater significance to pairs sharing more degrees in common. Since the maximum number of chords which PROGRS must arrange within any single segment is s6, significances of individual blandnesses are expressed as powers of 7 (lines 54-60). Array element BLNTMP(K) gives the blandness of the first K chords currently under consideration for the segment, while the variable LBN gives the blandness of the incumbent progression.

The method of evaluating statistical balance between the chords is intriguing because the program consults several values whose relative significances vary according to context. The values themselves are cumulative durations stored in array USETMP (this array bears no relation to the USETMP employed in subroutine CHORDS). Each time PROGRS selects a chord for a position, PROGRS augments the appropriate element of USETMP by the position's duration (line 48); conversely, PROGRS diminishes USETMP whenever it discards a chord (line 104). Array SCDTMP holds indices to each element of USETMP; a call in line 67 to the library subroutine LSORT sorts the contents of SCDTMP in descending order according to the contents of USETMP. This awards greatest significance to the largest cumulative durations. Arrays USECHD and SCDCHD hold cumulative durations and an associated schedule for the incumbent. Usage comparisons between candidates and incumbents are undertaken only when the program judges both progressions to be equally bland. PROGRS implements such comparisons by stepping through pairs of duration in order of significance until it finds a pair which differs. It then favors the chord (candidate or incumbent) with the smaller duration (lines 68-78).

Arpeggiation

Since subroutine ARPEGG very closely resembles its counterpart in program DEMO7, this subroutine is not reproduced here.

Comments

1. The first of my own writings to mention this search technique was the article describing my 1981 computer-composed Protocol for solo piano. At that time I called the technique “comparative evaluation”. Later in “Quantifying Musical Merit” (1992), the same technique is called “exhaustive search”, which term is employed by my 2011 production framework. The official AI term has been attributed to John McCarthy.