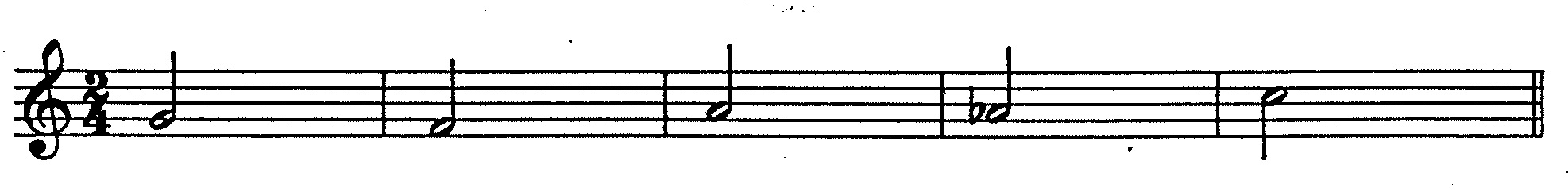Demonstration 8
A Functional Grammar

Introduction

Demonstration 8 provided the first of two practical components for Chapter 11: “Musical Design II: — Grammars” of my unpublished textbook on composing programs. It illustrates the method of generative grammars and, not coincidentally, the principle of top-down design. This method produces complex musical statements by starting with a fairly simple archetype and applying a set of fairly simple rewrite rules, also known as productions. The productions are applied recursively, which means that productions are capable of operating upon their own products.

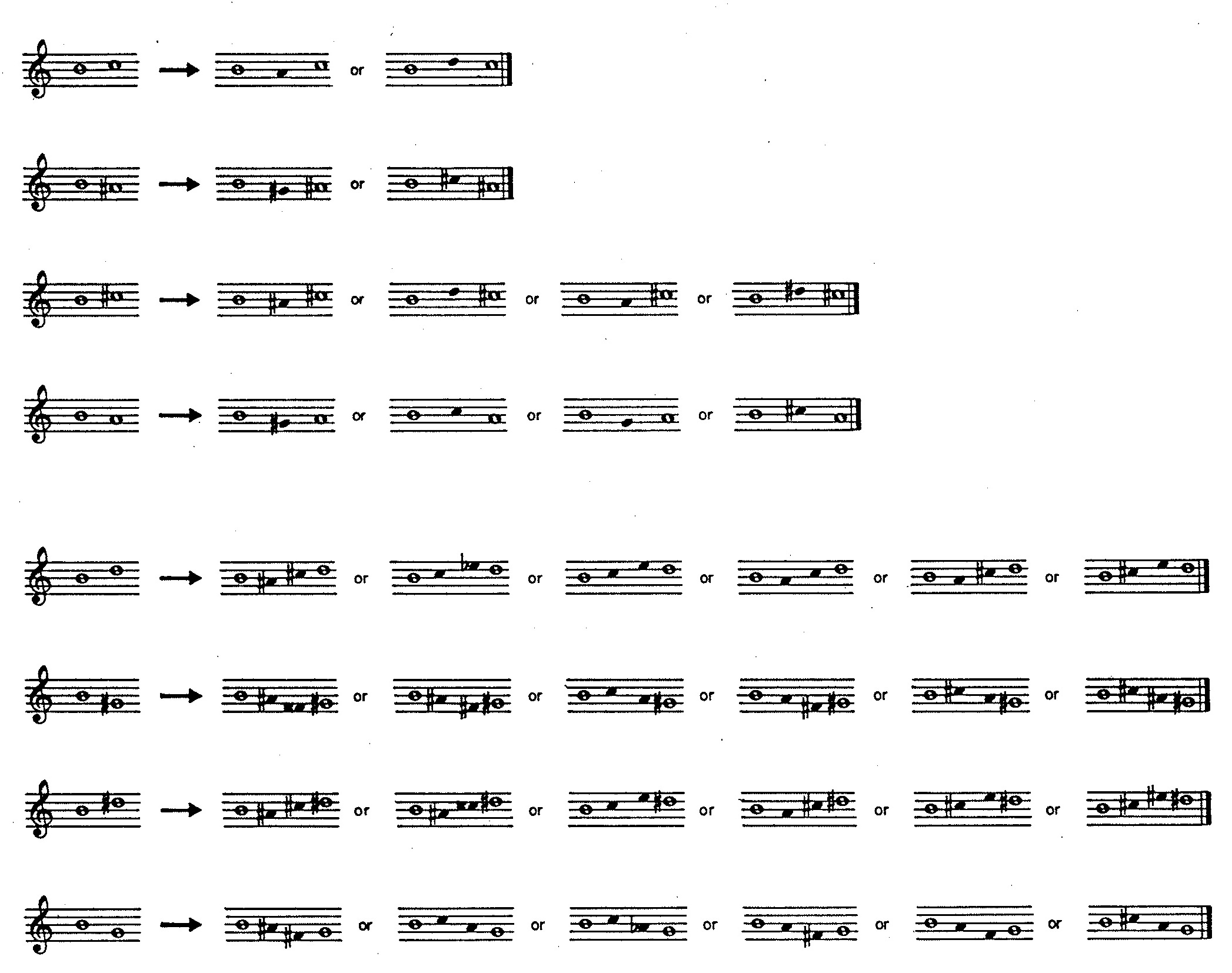
Demonstration 8 consists of three consecutive versions (variations) of a basic tune — or in linguistic jargon, three consecutive elaborations of an archetype. Each successive variation ornaments the tune by increasing orders of embellishment. The grammar of Demonstration 8 is ‘functional’ in the sense that the notes of the basic tune directly constitute grammatical units at the highest structural level, while all other notes may be regarded as ‘ornamental’ with varying levels of significance. The productions used to embellish both the basic tune and the higher-level ornaments are drawn from traditional formulae: seconds are embellished by either escaping tones or reaching tones; thirds by changing-note groups (“cambiata”).

Compositional Directives

The basic tune is illustrated in Figure 1 while the ornaments appear in Figure 2. Notice that the basic tune and each of the ornaments consist solely of seconds and thirds. It is this consistent property which enables the ornamenting process to be applied recursively up to five levels (counting the archetype as level 1): not only does the program elaborate upon the tune itself, but also upon the ornaments, upon the ornaments upon the ornaments, and so forth. Notes from the basic tune receive durations of 8 sixteenths; ornamental notes receive durations of 5, 3, 2, and 1 sixteenths, depending on their recursive levels.

The transcribed product appears in Figure 3.

Implementation

The trick to implementing top-down recursion in FORTRAN, which does not employ a system stack and which therefore does not permit self-referencing code modules, is to set up an explicit collection of parallel stacks so that all of the attributes characterizing a grammatical unit at an arbitrary level of recursion can be accessed using a single index.

Listing 1: Program DEMO8.		Listing 2: BLOCK DATA routine for DEMO8.

Program DEMO8 proper appears as Listing 1; the BLOCK DATA routine used to initialize COMMON memory variables appears as Listing 2.

The variable LEVEL provides a single stack pointer, while the various stacks indexed by this pointer are all implemented as arrays with names ending in LEV. Notice that LEVEL and its associated stack arrays are all declared in common memory, which makes them accessible both to DEMO8 proper and to the program's subroutines. Notice also that none of LEVEL and its associated stack arrays are initialized in the BLOCK DATA routine. These variables will provide active workspace whose content will frequently be overwritten.

Main Program

The following explanations seek to illustrate recursive grammars in play. The explanations are peppered with line numbers, but you are are by no means expected to chase down every line of code. Rather, you should follow through with line numbers only when you have a specific question that the narrative is not answering.

The loop spanning lines 16-26 is indexed by IVER. It iterates through Demonstration 8's three versions; line 19's call to subroutine COMPOS generates the individual versions. The only explicit parameter in this call is ITIME, which holds the current score time in thirty-second notes. Understand that FORTRAN passes subroutine arguments by address rather than by value, so that anything COMPOS does with ITIME also affects ITIME's value here in the main program. The variable Subroutine COMPOS takes the The three-element array EMBVER It also passes a value from array EMBVER to the first location of array EMBLEV; this value controls the number of nested ornaments.

Recursion

The heart of the compositional process is subroutine COMPOS, presented in Listing 3. Although the body of this subroutine is implemented as a loop (lines 23-49), this is not your normal iterative sequence. The loop indexing is bi-directional:

• Variable LEVEL iterates from the top down and back, where LEVEL=1 is topmost.
• Variable IDX iterates from left-to-right in the time dimension, where IDX=1 is leftmost.

To complicate things further, each change in LEVEL disrupts the left-to-right progression of IDX. Thus whenever COMPOS descends to a lower level, it needs set aside (“push”) the current value of IDX so that this value can be reclaimed (“pop”) once lower-level processing has completed. That is what a stack is for. In particular, array IDXLEV keeps track of IDX at the various recursive levels, while array CNTLEV stores corresponding limits. Each loop iteration begins first by advancing IDX one position to the right (line 25), then immediately tests (line 26) whether IDX has reached its limit. COMPOS descends to the next (deeper) level in line 40 and immediately thereafter initializes IDXLEV(LEVEL) to 0. COMPOS ascends to the previous (shallower) level in line 47, but the value of IDX is not reclaimed until the loop iterates (line 25).

COMPOS keeps track of the levels of levels of recursion, each of which ornaments a melodic fragment passed down from the previous level. The variable LEVEL indicates the level of recursion, array element CNTLEV(LEVEL) indicates how many items occur in a fragment, and array element IDXLEV(LEVEL) indicates which of these items is currently under consideration. For increased efficiency, COMPOS transfers this indicator to the holding variable IDX. The pitch of the current item is stored in array element PCHLEV(IDX,LEVEL). For LEVEL=1, COMPOS initializes PCHLEV to the basic tune (lines 13-18), which is specified to the program as array TUNE and populated in line 8 of the BLOCK DATA routine presented in Figure 4 (d). Items at lower levels may be either notes or rests; rests are represented as notes with null pitches. For each item but the last in a fragment, COMPOS performs the following actions:

1. If the current note or rest occurs at the current level of ornamentation, COMPOS directs subroutine WNOTE to append it to the human-readable listing (line 34 for rests, line 36 for notes). The duration of a note is stored in array element DURLEV(LEVEL) as populated in line 9 of the BLOCK DATA routine.
2. If (1) neither the current item nor its immediate successor are rests and if also (2) the limit (stored in array element EMBLEV(LEVEL)) has yet to be reached, then COMPOS does two things:
   1. COMPOS requests subroutine DEDUCE to select a possible ornament at the next level down (line 38)
   2. COMPOS then advances to the next recursive level (lines 40-41).

The last note in a fragment at the current level is the same as the next note in the fragment at the previous level, so COMPOS backtracks one level (lines 46-47) when IDX reaches CNTLEV(LEVEL).

Productions

Subroutine DEDUCE is presented in Listing 4. Although the subroutine has no formal arguments, information is passed along from subroutine DEDUCE through common memory variables. In particular, LEVEL gives the current level of recursion, LEVEL1 gives the level plus 1, IPCH1 gives the origin pitch, and IPCH2 gives the goal pitch. For each pair of consecutive pitches passed to it either by subroutine COMPOS, or by a prior level of recursion, subroutine DEDUCE first decides whether or not to ornament at the current level.

For each pair of consecutive pitches passed to it either by subroutine COMPOS, or by a prior level of recursion, subroutine DEDUCE first decides whether or not to ornament at the current level. If so DEDUCE first identifies a repertory of suitable ornaments, then chooses a specific ornament from this repertory.

Decision to Ornament

The decision to ornament (lines 24-31) is a yes-or-no trial which incorporates feedback from corresponding trials at higher levels.¹ Line 24 executes this decision with a call to the library function SUCCES where the probability of a positive outcome is EMBLEV(LEVEL)/FLOAT(MLEV1-LEVEL). Here the numerator reflects how many choices-to-ornament are to be made from the current recursive level on down, while the denominator reflects the number of levels remaining, and thus the number of opportunities left.

• If the trial chooses to ornament at the present level, then one fewer positive choice must occur in levels remaining; hence line 31 sets EMBLEV(LEVEL1) = EMBLEV(LEVEL)-1.0. DEDUCE then proceeds to select which ornament to apply.
• If the trial chooses not to ornament, then the remaining positive choices must occur in levels remaining; hence line 26 sets EMBLEV(LEVEL1) = EMBLEV(LEVEL). DEDUCE then skips the remaining actions and returns immediately to COMPOS.

Repertory

If it decides in favor of ornamenting an interval at the current level, lines 35-44 of DEDUCE determine what kind of interval it must ornament. It locates a repertory of ornaments for this level among the eight repertories illustrated in Figure 2. All ornamental pitches are expressed (lines 12-19) in array ORNMNT as offsets from the origin pitch. How this data is accessed exemplifies the index gymnastics needed to represent non-rectangular data in FORTRAN arrays. For each of the eight intervals, array PTRORN holds a pointer (array index) indicating which element of ORNMNT holds the first offset for the first ornament in the repertory corresponding to the indicated interval. Array INCORN holds the number of ornamental pitches (1 for escaping or reaching tones, 2 for changing-note groups); incrementing the pointer by this number gives successive ornaments in the repertory. Array NUMORN indicates the number of ornaments in the repertory.

For example, Table 1 dereferences from ORNMNT the various ornaments which would apply to the second interval in Figure 1. This interval ascends from TUNE(2)=53 (F4) to TUNE(3)=57 (A4). The pitch number 53 comes into DEDUCE through the common variable IPCH1, while the pitch number 57 comes through IPCH2. Line 35 calculates the index I into arrays PTRORN, INCORN, and NUMORN as IPCH2-IPCH1+5=57-53+5=4+5=9. Array element PTRORN(9) contains the index value 37. This is the leftmost position in the seventh line of the multi-line data statement which initializes ORNMNT (line 18 of the listing). The number of ornamental pitches in the present example INC is INCORN(9)=2, which is why Table 1 dereferences ORNMNT elements in pairs. The number of ornaments NUM is NUMORN(3)=6; therefore Table 1 dereferences six ornaments. These ornaments correspond to the second-from-bottom line of staves in Figure 2. The six indices 37, 39, 41, 43, 45, and 47 are gathered into the scheduling array SCHED.

Instance

Once it has established a schedule of pointers to ornaments, the next step is to select a specific ornament. DEDUCE does this in lines 48-61. Selection is heuristic with cumulative feedback, driven by chromatic usage. This process is uncomplicated by constraints, since the ornaments listed in SCHED are precisely those deemed suitable for the present context.² A complication does exist, however, and this is posed by the changing-note groups: how to reconcile the contributions from two separate chromatic numbers. The tactic for reconciling such competing influence is called the minimax principle.

Referring to Table 1, consider the ornament E4-G#4 in row 2 and the ornament E!4-G4 in row 4. Assume that E and G# have been moderately used, that E! has been lightly used, and that G4 has been heavily used. Since G4 has already been heavily used, choosing E!4-G4 would throw G4 even more strongly out of balance, despite the leveling effect of using an E. Thus E4-G#4 is the more sensible choice. Thus the minimax principle at work, in a rudimentary way.

The first thing is to eliminate any bias introduced by the physical sequence of ornaments in array ORNMNT. This was started by gathering indices into array SCHED (previous step). Bias-elimination continues in line 44 by calling the library routine SHUFLE to randomize the content-order in SCHED and in line 51 by using the index IDXORN of the ornament-evaluating loop to dereference an ornament locator LPTR from SCHED(IDXORN).

Program DEMO08 maintains statistics of chromatic usage in the 12-element array CUMDEG, made visible to DEDUCE through common memory. Within the current code segment, variable CUM0 holds the smallest CUMDEG value discovered for an ornament so far; this variable is set very large in line 48 and is reduced in line 58 each time a more preferable ornament is discovered. Similarly, variable CUM1 holds the largest CUMDEG value discovered for the candidate ornament; this variable is set very small in line 50 and is increased in line 54 each time a larger CUMDEG value is discovered. Coming out of this code segment, an index to the selected ornament has been placed in variable IPTR.

Having selected an ornament, the next step is to marshal details about the ornament, plus its bracketing origin and goal pitches, into the PCHLEV stack for transmission to the next level of recursion. This happens in lines 65-76. The circumstance of extracting individual pitches for the ornament also makes this a convenient place to increment chromatic usage in CUMDEG. Notice in line 72 that the incrementing amount is provided by DURLEV(LEVEL+1). Thus upon program completion CUMDEG(I) will reflect not the total count of notes employing the Ith chromatic degree, but rather the combined duration of such notes.

Insert a Rest

The final action DEDUCE happens in lines 80-91. This code employs a Bernoulli trial to decide whether or not to include a rest in the ornament. If the trial outcome is favorable, then DEDUCE inserts a rest between two consecutive notes of the ornamented fragment.

Comments

1. Modeled on the RATIO feature of G.M. Koenig's Project Two.
2. Actually not. A range check should have been implemented.