Demonstration 3
Statistical Frames

Introduction

I have coined the term statistical frame to identify a practice already well established in the tradition of composing programs. This practice acknowledges that direct random selection relies upon the laws of large numbers to bring the actual values selected into conformance with the distribution of values intended. That reliance proves to be very weak indeed.1

The method of statistical frames puts statistical conformity above unpredictability, thus defying the the gambler's fallacy. A statistical frame is a local region within a composition within which a distribution holds sway absolutely. A classic example of the method is twelve-tone music, where a composer accepts the discipline of using all twelve degrees of the chromatic scale before any specific degree may be re-used. Another example is the approach employed manually by Iannis Xenakis to craft the work Achorripsis (as distinguished from the direct randomness employed in his Stochastic Music Program). The same approach figures prominently in composing programs developed by Gottfried Michael Koenig, especially Project Two.

Demonstration 3 provided the practical component for Chapter 4: “Random Selection II — Statistical Frames” of my unpublished textbook on composing programs. It illustrates an automated compositional process employing statistical frames. Using the techniques developed thus far, the most effective solution is to sample randomly shuffled pools. Like Demonstration 2, compositional control over Demonstration 3 is limited to prescribing distributions affecting attributes of phrases and notes. However, statistical pool generation and shuffling insure much tighter adherence to these distributions than had been possible using direct random selection.

 
Figure 1 (a): Distribution of phrase durations.   Figure 1 (b): Distribution of average note durations.
     
 
Figure 1 (c): Distribution of phrase articulations.   Figure 1 (d): Distribution of phrase center pitches.

Compositional Directives

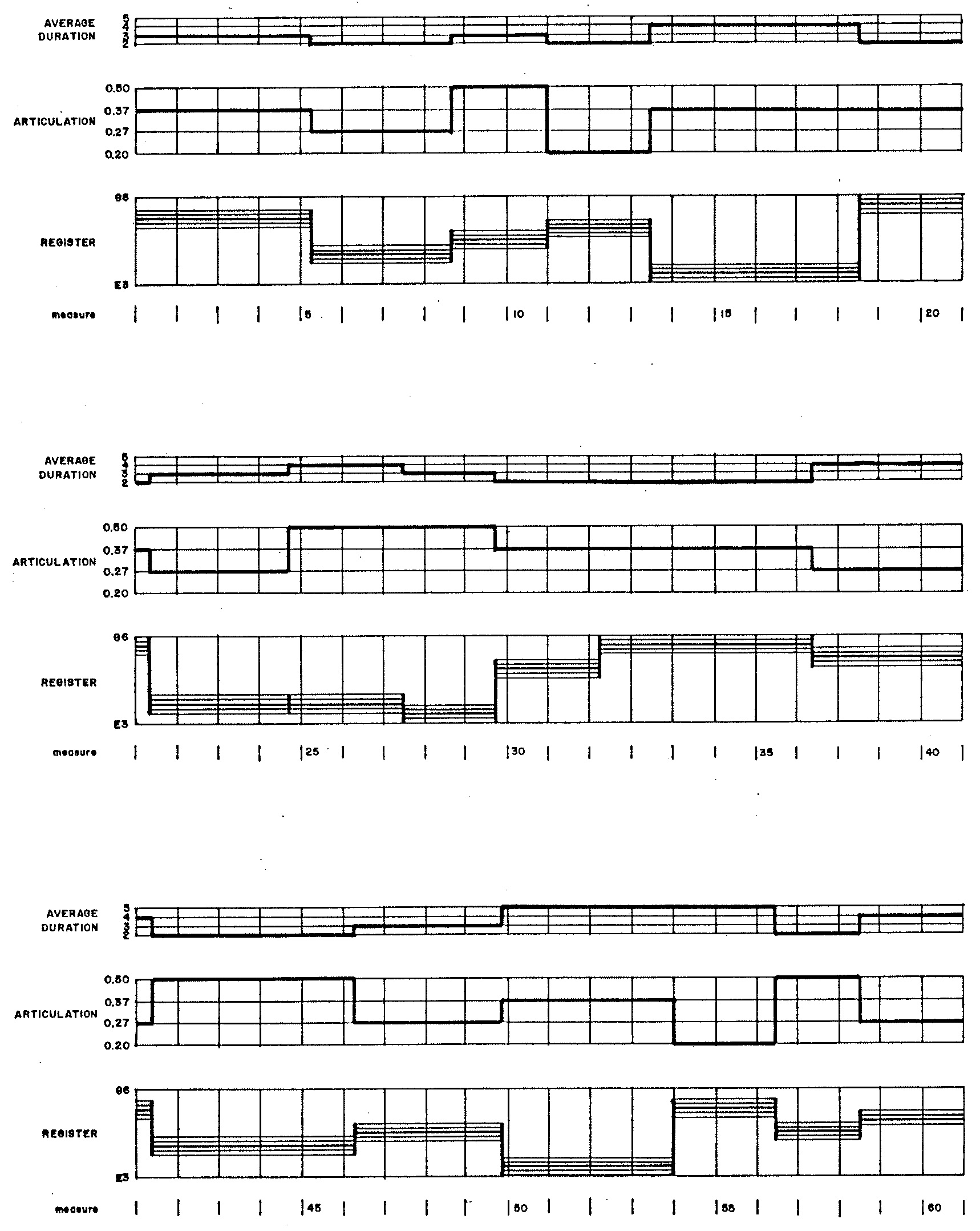
The distributions of musical attributes affecting phrases in Demonstration 3 are depicted in Figure 1 (a) (durations), Figure 1 (b) (average note durations), Figure 1 (c) (articulations), and Figure 1 (d) (center pitches). The most prominent stylistic trait distinguishing Demonstration 3 from Demonstration 2 is that where Demonstration 2 exploited the twelve chromatic degrees with equal probability, Demonstration 3 exploits gamuts of only nine adjacent semitones within a given phrase, weighting pitches at the center of a gamut three times more strongly than it weights the outer pitches.

 
Figure 2 (a): Distribution of note durations.   Figure 2 (b): Distribution of pitch deviations.

The distributions of musical attributes affecting notes in Demonstration 3 are depicted in Figure 2 (a) (durations) and Figure 2 (b) (chromatic degrees). Figure 3 graphs the musical attributes selected for phrases.


Figure 3: Profile of Demonstration 3.

Figure 3 graphs the musical attributes selected for phrases.


Figure 4: Transcription of Demonstration 3.

A transcription of the musical product appears in Figure 4.

Implementation

The explanations to follow focus variously on four attributes of phrases and three attributes of notes. The purpose is to tease out the strands of code that affect a particular attribute, and thus to reveal the mechanics of statistical frames in play. The explanations are peppered with line numbers, but you are are by no means expected to chase down every line of code. Rather, you should follow through with line numbers only when you have a specific question that the narrative is not answering.

Program DEMO3 is reproduced in Listing 1 while its particular version of subroutine PHRASE appears in Listing 2. Like program DEMO2, DEMO3 reflects the musical structure of phrases and notes as a design of nested loops. An outer phrase-composing loop in DEMO3 proper and an inner note/rest loop in subroutine PHRASE.


Listing 1: Program DEMO3.

Program DEMO3 proper implements the phrase-composing loop in lines 43-58. Variables and arrays pertaining to phrase attributes adhere to four root abbreviations:

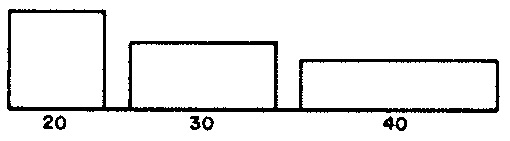
  1. PHR — length of phrase. Parameter MPHR fixes the pool length for phrase lengths at 13 (line 5); line 13 populates 3 specific values into array VALPHR, populates the corresponding weights from Figure 1 (a) into array WGTPHR, and initializes the sum of these weights into variable SUMPHR. Line 31's call to subroutine FILL expands the 3 values in VALPHR into 13 values in the pool array POLPHR. Line 45's call to subroutine SERIES steps through array POLPHR in shuffled order selecting specific lengths for phrases. This result is placed in variable IPHR.
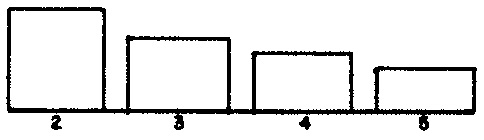
  2. AVG — average duration of notes (equivalently, average tempo) within a phrase; the average duration of rests is half as large. Parameter MAVG fixes the pool length for average durations at 19 (line 5); line 14 populates 4 specific values into array VALAVG, populates the corresponding weights from Figure 1 (b) into array WGTAVG, and initializes the sum of these weights into variable SUMAVG. Line 33's call to subroutine FILL expands the 4 values in VALAVG into 19 values in the pool array POLAVG. Line 50's call to subroutine SERIES steps through array POLAVG in shuffled order selecting average note durations for phrases. This result is placed in variable AVGDUR.
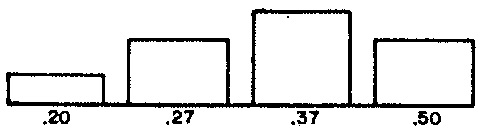
  3. ART — articulation within a phrase, expressed as the probability that a rhythmic unit will serve as a rest. Parameter MART fixes the pool length for average durations at 8 (line 5); line 18 populates 4 specific values into array VALART, populates the corresponding weights from Figure 1 (c) into array WGTART, and initializes the sum of these weights into variable SUMART. Line 35's call to subroutine FILL expands the 4 values in VALART into 8 values in the pool array POLART. Line 52's call to subroutine SERIES steps through array POLAVG in shuffled order selecting articulations for phrases. This result is placed in variable ARTIC.
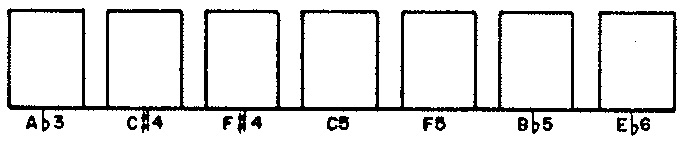
  4. REG — register within a phrase, expressed as the central pitch in a nine-semitone gamut. Parameter MREG fixes the pool length for registers at 8 (line 5). Since the weights in Figure 1 (d) are uniform, line 19 explicitly populates the pool array POLREG. Selection of registers for phrases is therefore quasi-serial, all 8 distinct registers must be used before any register may be repeated. Line 52's call to subroutine SERIES steps through array POLREG in shuffled order selecting registers for phrases. This result is placed in variable IREG.

The phrase-composing loop completes by calling subroutine PHRASE in line 56.


Listing 2: Subroutine PHRASE.

Subroutine PHRASE implements the note-rest loop. Line 9 decides whether the current iteration should generate a note or a rest. If a note is elected, lines 11-15 choose the note's duration and chromatic The note/rest loop completes by calling subroutine WNOTE in line 36

Rhythm

Variables and arrays pertaining to choosers for note/rest trials have names ending in UNF. Each note-rest chooser value is uniformly distributed between zero and one. The pool for choosers is configured in DEMO03 proper. Parameter MUNF fixes the pool length for choosers at 20 (line 6); line 19 explicitly populates the pool array POLUNF. This means that all 20 distinct note-rest choosers must be used before any chooser may be repeated. Moving down into subroutine PHRASE, line 50's call to subroutine SERIES steps through array POLUNF in shuffled order selecting choosers for note/rest trials. This result is placed in variable R.

Variables and arrays pertaining to note durations and rest durations have names ending in DUR. The pool for note durations is configured in DEMO03 proper. Parameter MUNF fixes the pool length for note/rest durations at 10 (line 6). The pool array POLDUR is declared in line 9. Line 37's call to subroutine FILL expands two distribution parameters into 10 values in the pool array POLDUR. Of the two distribution parameters, setting the average duration to unity allows average note durations to be applied later, within phrases. Setting the max/min proportion to 1000 indicates that this action should strive toward the pure negative-exponential distribution graphed in Figure 2 (a). Moving down into subroutine PHRASE, line 19's call to subroutine SERIES steps through array POLDUR in shuffled order selecting note/rest durations. This result is scaled by the average note duration (variable AVGDUR) and placed in variable DUR.

Pitches

Variables and arrays pertaining to deviations from a phrase's central pitch have names ending in PCH. The pool for pitch deviations is configured in DEMO03 proper. Parameter MPCH fixes the pool length pitch deviations at 40 (line 6); lines 15-17 populates 9 specific values into array VALPCH, populates the corresponding weights from Figure 2 (b) into array WGTPCH, and initializes the sum of these weights into variable SUMPCH. Line 31's call to subroutine FILL expands the 9 values in VALPCH into 40 values in the pool array POLPCH. Moving down into subroutine PHRASE, line 24's call to subroutine SERIES steps through array POLPCH in shuffled order selecting pitch deviations. This result is combined with the register (variable IREG) and placed in variable IPCH.

Shuffling a Pool

The library subroutine SHUFLE randomly shuffles a supply of values. Calls to SHUFLE require two arguments:

  1. VALUE — Supply of values. VALUE must be an array whose dimension in the calling program is NUM (argument #2 below).
  2. NUM — Number of supply elements (dimension of array VALUE in the calling program).

SHUFLE works by stepping backwards through the supply, leveraging the library function IRND to exchange each supply element either with itself or with a leftward element.2

Sampling a Pool

The library subroutine SERIES3 samples a supply of values shuffling the supply contents after each cycle. It is modeled on the SERIES feature of Koenig's Project Two. Calls to SERIES require four arguments:

  1. RESULT — SERIES selects a supply value and returns the value in this location.
  2. VALUE — Supply of values. Duplicate values are not permitted. VALUE must be an array whose dimension in the calling program is NUM (argument #4 below).
  3. IDX — Index to pending selection. IDX must be an integer in the calling program. Before anything else, SERIES increments IDX by 1. Whenever IDX threatens to exceed NUM, SERIES leverages subroutine SHUFLE to shuffle the VALUE array, then wraps IDX back around to 1. SERIES completes by setting RESULT=VALUE(IDX). Initializing IDX to 0 causes SERIES present the supply in its original order. If you want SERIES to shuffle the supply right at the outset, initialize IDX to NUM.
  4. NUM — Number of supply elements (dimension of array VALUE in the calling program).

Populating a Weighted Pool

The library subroutine FILL4 populates a supply of values conforming to a discrete table of weights. Calls to FILL require six arguments:

  1. POOL — Statistical pool. POOL must be an array whose dimension in the calling program is LENGTH (argument #6 below). The contents of this array will be overwritten with each call to FILL.
  2. VALUE — Supply of values. Duplicate values are not permitted. VALUE must be an array whose dimension in the calling program is NUM (argument #5 below).
  3. WEIGHT — Array of weights associated with each member of VALUE. VALUE must be a real array whose dimension in the calling program is NUM, whose contents are all non-negative. At least one weight must be positive.
  4. SUM — Sum of weights stored in array WEIGHT. SUM must be a real variable in the calling program with a value greater than zero.
  5. LENGTH — Number of samples to be assembled in array POOL. LENGTH must be a positive integer.
  6. NUM — Number of supply values in array VALUE. NUM must be a positive integer.

FILL operates in an active generation phase and a passive transformation phase. The generation phase produces LENGTH values equally spaced (and therefore uniformly distributed) over the range from zero to unity. The transformation phase uses a method adapted from subroutine SELECT, where the values from zero to unity become choosers against the WEIGHT array.

Populating a Duration Pool

The library subroutine FILLX5 populates a supply of values conforming to John Myhill's generalization of the negative exponential distribution. Calls to FILLX require four arguments:

  1. POOL — Statistical pool of durations. POOL must be a real array whose dimension in the calling program is LENGTH (argument #4 below). The contents of this array will be overwritten with each call to FILLX.
  2. AVG — Average value. AVG must be a real number in the calling program whose value is positive.
  3. PROPOR — Maximum result divided by minimum result. PROPOR must be a real number in the calling program whose value is 1.0 or greater. With this argument near unity, results will cluster around AVG. As PROPOR increases, results come to resemble pure negative exponential randomness.
  4. LENGTH — Number of durations to be assembled in array POOL. LENGTH must be a positive integer.

To learn more of the workings of negative exponential randomness and of Myhill's generalization, see the references provided for function RANX.

Comments

  1. I undertook empirical comparisons between populations generated by direct random selection and populations generated by more rigorous statistical methods. These comparisons were the basis of a two-part article on “Thresholds of Confidence” in Leonardo Music Journal, Part 1: Theory and Part 2: Practice.
  2. The algorithm for random shuffling was developed by Moses and Oakford in 1963 and independently by Durstenfield in 1964; it came to me through Donald Knuth's Seminumerical Algorithms. The FORTRAN source code for subroutine SHUFLE appears in Automated Composition, Chapter 5, pp. 5-8 to 5-9.
  3. The FORTRAN source code for subroutine SERIES appears in Automated Composition, Chapter 5, pp. 5-9 to 5-10.
  4. The mechanics of subroutine FILL are discussed under the “Saturated Frames’ topic on page 59 of my “Catalog of Sequence Generators” The FORTRAN source code for subroutine FILL appears in Automated Composition, Chapter 5, pp. 5-6 to 5-8.
  5. Subroutine FILLX is presented in Automated Composition, Chapter 5, pp. 5-5 to 5-6.

© Charles Ames Original Text: 1984-11-01 Page created: 2017-03-12 Last updated: 2017-03-12