Waveform Reference for Sound-Synthesis

Overview

This page enumerates waveform families which can be used for digital sound synthesis. Several of these waveforms (sine, sawtooth, square, triangle, pulse) were selectable options on the original analog tone generators. Sample tones have been provided for each waveform graph.

When this page was originally posted, my intent was to make sound synthesis accessible to all through Java applets, which included an Orchestra Editor, a Note-List Editor, and a Wave-file viewer. Since browers have now withdrawn support for applet technology I have had to fall back to a desktop application. For those with access to this application, I have prepared an orchestra file, WaveformOrch.xml. This file contains most of the waveforms graphed on this page (excepting rectangle waves, for reasons explained below). The file also defines a simple oscillator instrument which obtains the waveform number parametrically. The “Test ID” indicated under each graph identifies both the waveform number in WaveformOrch.xml and the corresponding test tone number. For instructions, see Viewing the Waveform Orchestra.

The waveforms described on this page have been created with a consistent length of 512 samples. As explained in the discussion of foldover, the highest harmonic representable by a waveform of length 512 is the 256th harmonic, since at least one sample is required for the up phase, and at least one other sample is required for the down phase. Since the waveforms actually illustrated on this page extend no higher than the 16th harmonic, this in fact allocates 512/16 = 32 samples for up and down phases combined. Which is good.

At the audio CD-standard sampling rate of 44100 samples per second, the highest frequency which may be generated is 22050 Hz. Having a waveform with 16 harmonics additionally limits this ceiling to 22050/16 =1378 Hz., which rounds down to E6 (the E two octaves and a third above middle C). For pitches in the range from F6 to E7, waveforms should be limited to 8 harmonics. Four harmonics is the limit between F7 and E8. Two harmonics is the limit between F8 and E9. C10, at 16744 Hz., is outside the range of most human hearing.

Sine Wave

The sine wave represents the purest tone. It has exactly one harmonic, which is the fundamental.

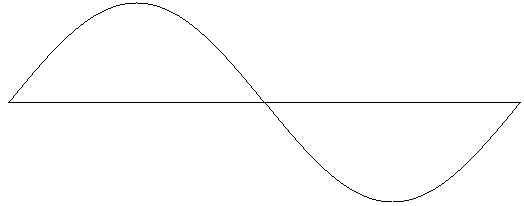
Figure 1: Sine wave. Test ID: 1. To hear a realization, click here.

Sawtooth Wave

In the sawtooth family of waveforms, the amplitude of each harmonic descends as the inverse of the harmonic number.

Harmonic	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Amplitude	1.000	0.500	0.333	0.250	0.200	0.167	0.143	0.125	0.111	0.100	0.091	0.083	0.077	0.071	0.067	0.063

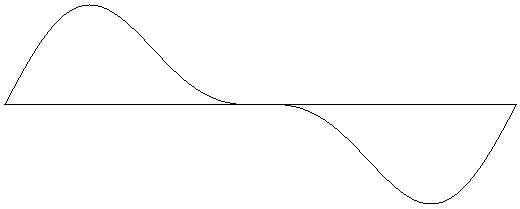
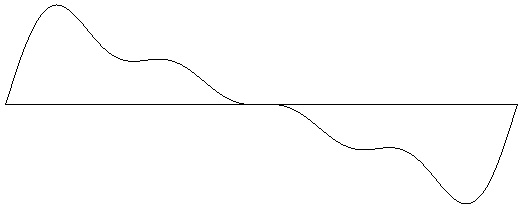
Figure 2-1: Sawtooth wave with 2 harmonics (one octave). Test ID: 202. To hear a realization, click here.	Figure 2-2: Sawtooth wave with 4 harmonics (two octaves). Test ID: 204. To hear a realization, click here.
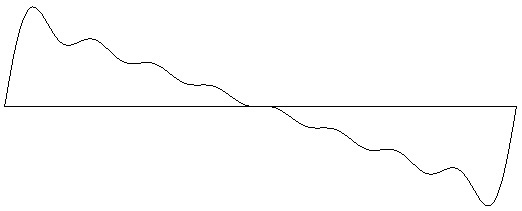
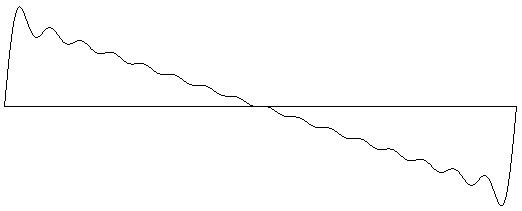
Figure 2-3: Sawtooth wave with 8 harmonics (three octaves). Test ID: 208. To hear a realization, click here.	Figure 2-4: Sawtooth wave with 16 harmonics (four octaves). Test ID: 216. To hear a realization, click here.

Rounded-Sawtooth Wave

In the rounded-sawtooth family of waveforms, the amplitude of each harmonic descends as the squared inverse of the harmonic number. The rounded-sawtooth wave is to the sawtooth wave as the triangle wave is to the square wave.

Harmonic	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Amplitude	1.000	0.250	0.111	0.063	0.040	0.028	0.020	0.016	0.012	0.010	0.008	0.007	0.006	0.005	0.004	0.004

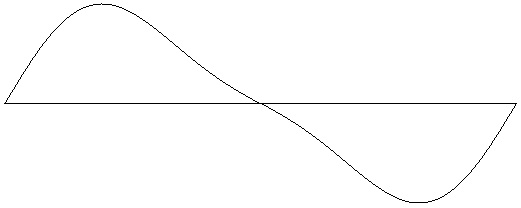
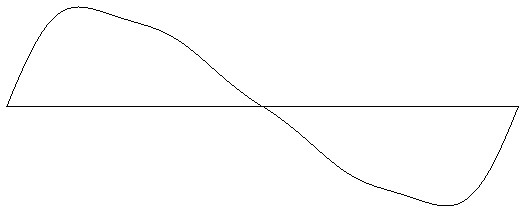
Figure 4-1: Rounded-sawtooth wave with 2 harmonics (one octave). Test ID: 302. To hear a realization, click here.	Figure 4-2: Rounded-sawtooth wave with 4 harmonics (two octaves). Test ID: 304. To hear a realization, click here.
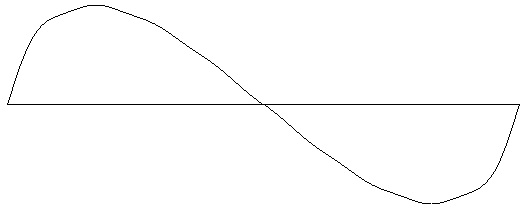
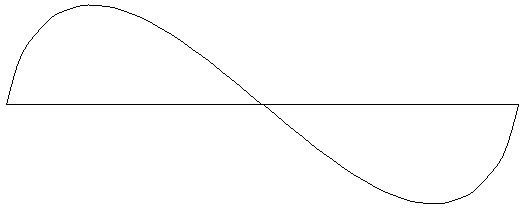
Figure 4-3: Rounded-sawtooth wave with 8 harmonics (three octaves). Test ID: 308. To hear a realization, click here.	Figure 4-4: Rounded-sawtooth wave with 16 harmonics (four octaves). Test ID: 316. To hear a realization, click here.

Square Wave

In the square family of waveforms, only the odd harmonic numbers are present. The amplitude of each harmonic descends as the inverse of the harmonic number.

Harmonic	1	3	5	7	9	11	13	15
Amplitude	1.000	0.333	0.200	0.143	0.111	0.091	0.077	0.067

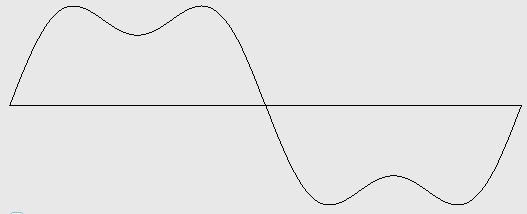
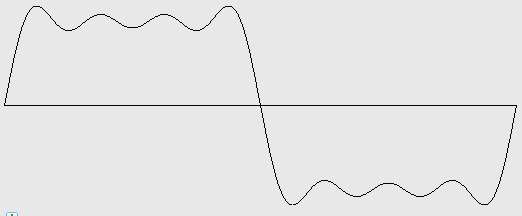
Figure 3-1: Square wave with harmonics 1 and 3 (2 octaves). Test ID: 403. To hear a realization, click here.	Figure 3-2: Square wave with harmonics 1, 3, 5, and 7 (3 octaves). Test ID: 407. To hear a realization, click here.
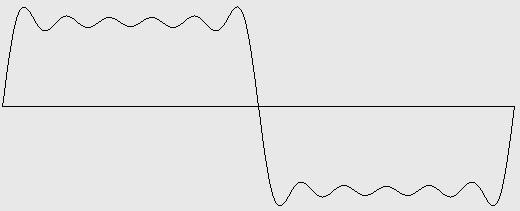
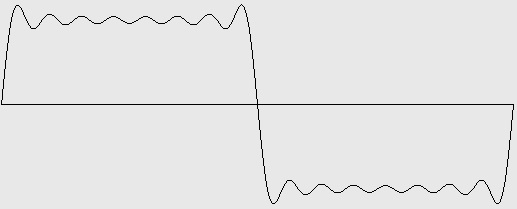
Figure 3-3: Square wave with harmonics 1, 3, 5, 7, 9, and 11 (3 ½ octaves). Test ID: 411. To hear a realization, click here.	Figure 3-4: Square wave with harmonics 1, 3, 5, 7, 9, 11, 13, and 15 (4 octaves). Test ID: 415. To hear a realization, click here.

Triangle Wave

In the triangle family of waveforms, only the odd harmonic numbers are present. The amplitude of each harmonic descends as the squared inverse of the harmonic number. Also, harmonics 3, 7, 11, 15, etc. are phase shifed by 180°.

Harmonic	1	3	5	7	9	11	13	15
Amplitude	1.000	0.111	0.040	0.020	0.012	0.008	0.006	0.004
Phase	0.0	0.5	0.0	0.5	0.0	0.5	0.0	0.5

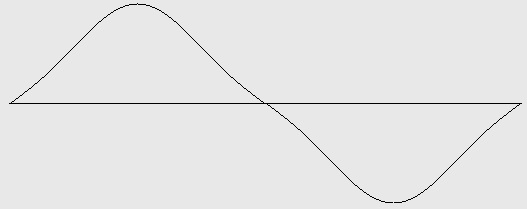
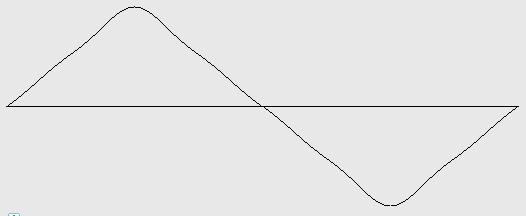
Figure 5-1: Triangle wave with harmonics 1 and 3 (2 octaves). Test ID: 503. To hear a realization, click here.	Figure 5-2: Triangle wave with harmonics 1, 3, 5, and 7 (3 octaves). Test ID: 507. To hear a realization, click here.
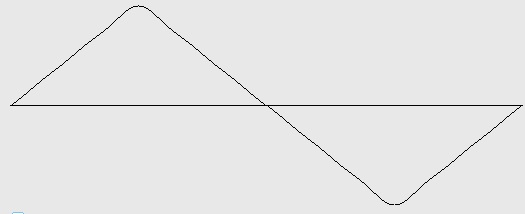
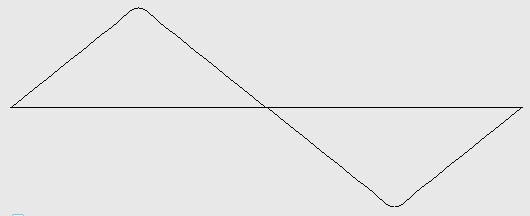
Figure 5-3: Triangle wave with harmonics 1, 3, 5, 7, 9, and 11 (3 ½ octaves). Test ID: 511. To hear a realization, click here.	Figure 5-4: Triangle wave with harmonics 1, 3, 5, 7, 9, 11, 13, and 15 (4 octaves). Test ID: 515. To hear a realization, click here.

Here is what a triangle wave looks like when you set all phases to 0°. Theory says that phase makes no difference. You can confirm or deny that theory by comparing test tone #515 with test tone #615 in WaveformOrch.xml.

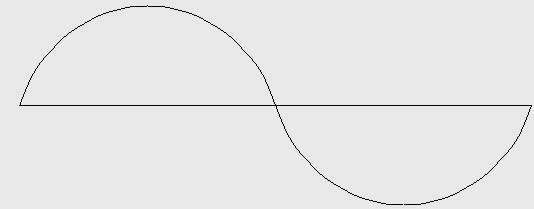
Figure 6: Waveform with harmonics 1, 3, 5, 7, 9, 11, 13, and 15 (4 octaves), inverse squared amplitudes, but all 0° phase values. Test ID: 615. To hear a realization, click here.

Pulse Wave

In the pulse family of waveforms, all harmonics have equal amplitude. The result is a buzzing sound not unlike the human glottis, which makes pulse waves essential for speech synthesis.

Harmonic	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Amplitude	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000	0.100	1.000	1.000	1.000	1.000	1.000	1.000

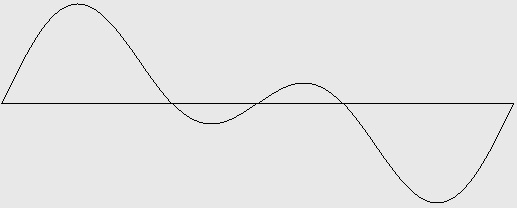
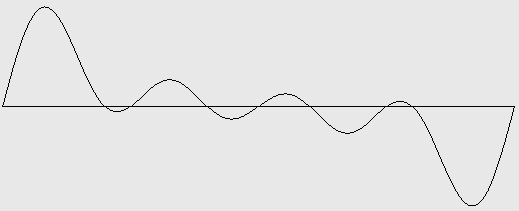
Figure 7-1: Pulse wave with 2 harmonics (one octave). Test ID: 702. To hear a realization, click here.	Figure 7-2: Pulse wave with 4 harmonics (two octaves). Test ID: 704. To hear a realization, click here.
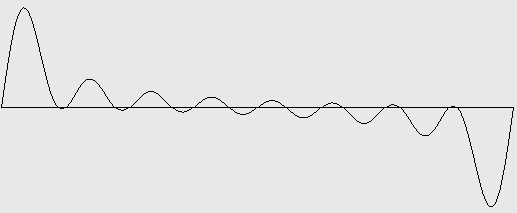
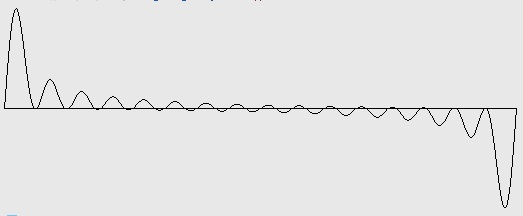
Figure 7-3: Pulse wave with 8 harmonics (three octaves). Test ID: 708. To hear a realization, click here.	Figure 7-4: Pulse wave with 16 harmonics (four octaves). Test ID: 716. To hear a realization, click here.

Rectange Wave

Rectangle waves generalize square waves by making portion of the waveform spent in the ‘up’ phase controllable. The control parameter is known as the duty cycle. So for example a rectangle wave with a 50% duty cycle is a square wave. A rectangle with a 25% duty cycle spends 1/4 of its wave cycle in the up position and 3/4 of its wave cycle in the down position. A 25% rectangle wave sounds exactly like a 75% rectangle wave. The limiting case of a rectangle wave as the duty cycle approaches zero is a pulse wave; however when the duty cycle actually reaches 0%, silence results.

Figure 8: Rectangle-wave generator.

The Wikipedia article on pulse waves actually concerns itself with the waveforms described here as rectangle waves. This article gives the following instructions for calculating rectangular waveforms:

A [rectangle] wave can be created by subtracting a sawtooth wave from a phase-shifted version of itself. If the sawtooth waves are bandlimited, the resulting [rectangle] wave is bandlimited, too. Another way to create one is with a single ramp wave (sawtooth or triangle) and a comparator, with the ramp wave on one input, and a [constant] threshold on the other. The result will be a precisely controlled pulse width, but it will not be bandlimited.

The Sound waveform manager requires waveforms to be described by adding together just one harmonic for each harmonic number — you can't specify two phase-shifted instances of the same harmonic. There is undoubtedly a formula giving the harmonic intensities for a rectangle waveform with whatever duty factor, but I don't know it. However, it is simple enough to implement Wikipedia's instructions within an audio processing instrument using the configuration shown in Figure 8. The essential units are an oscillator generating a sawtooth wave, a delay line to phase-shift the oscillator output, and a subtract operator. And this implementation has the advantage that swapping control signals for P8, P10, and V1 gives you dynamic timbre modulation.

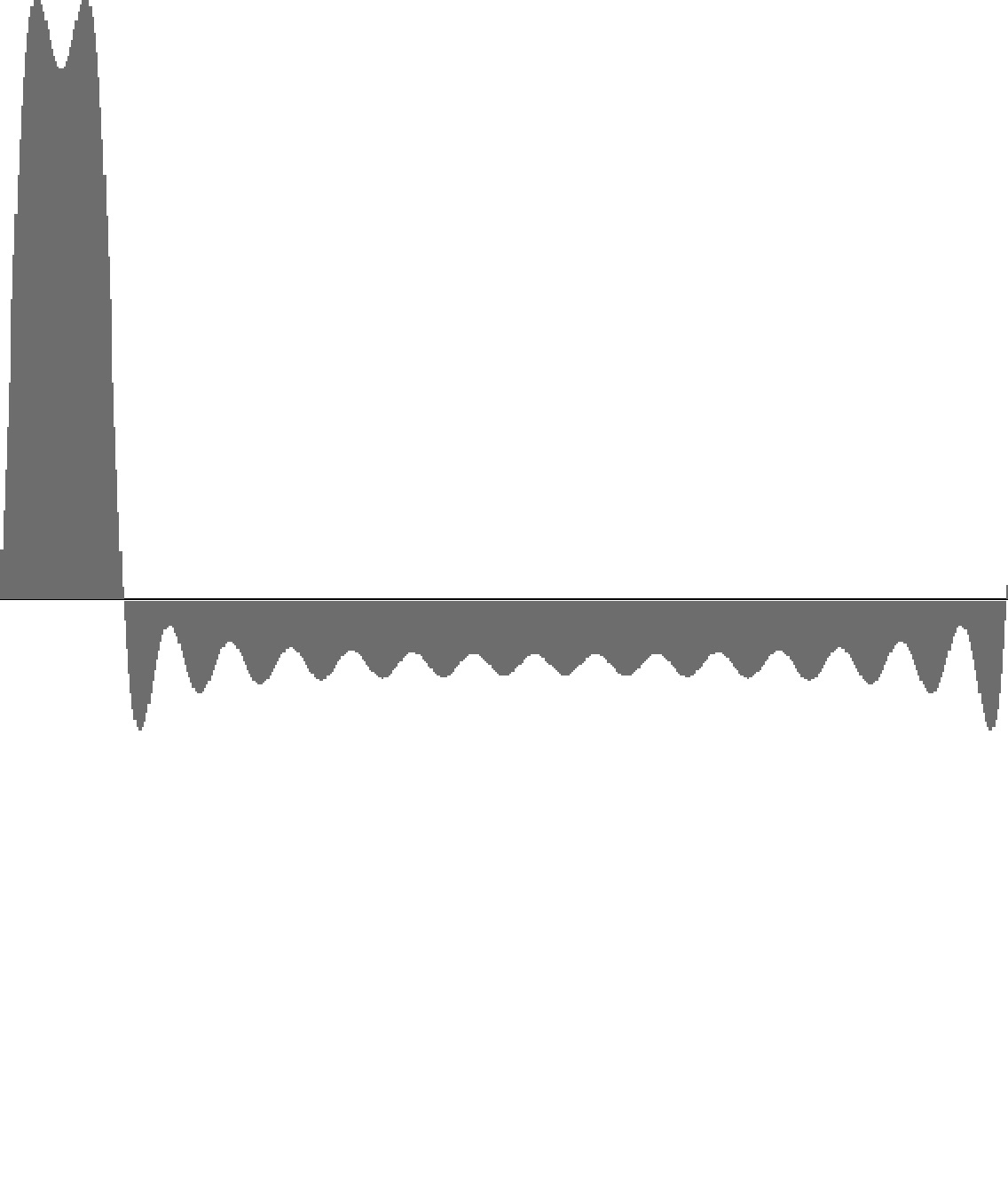
Figure 9-1: Rectangle wave with 16 harmonics and 10% duty factor. To hear a realization, click here.

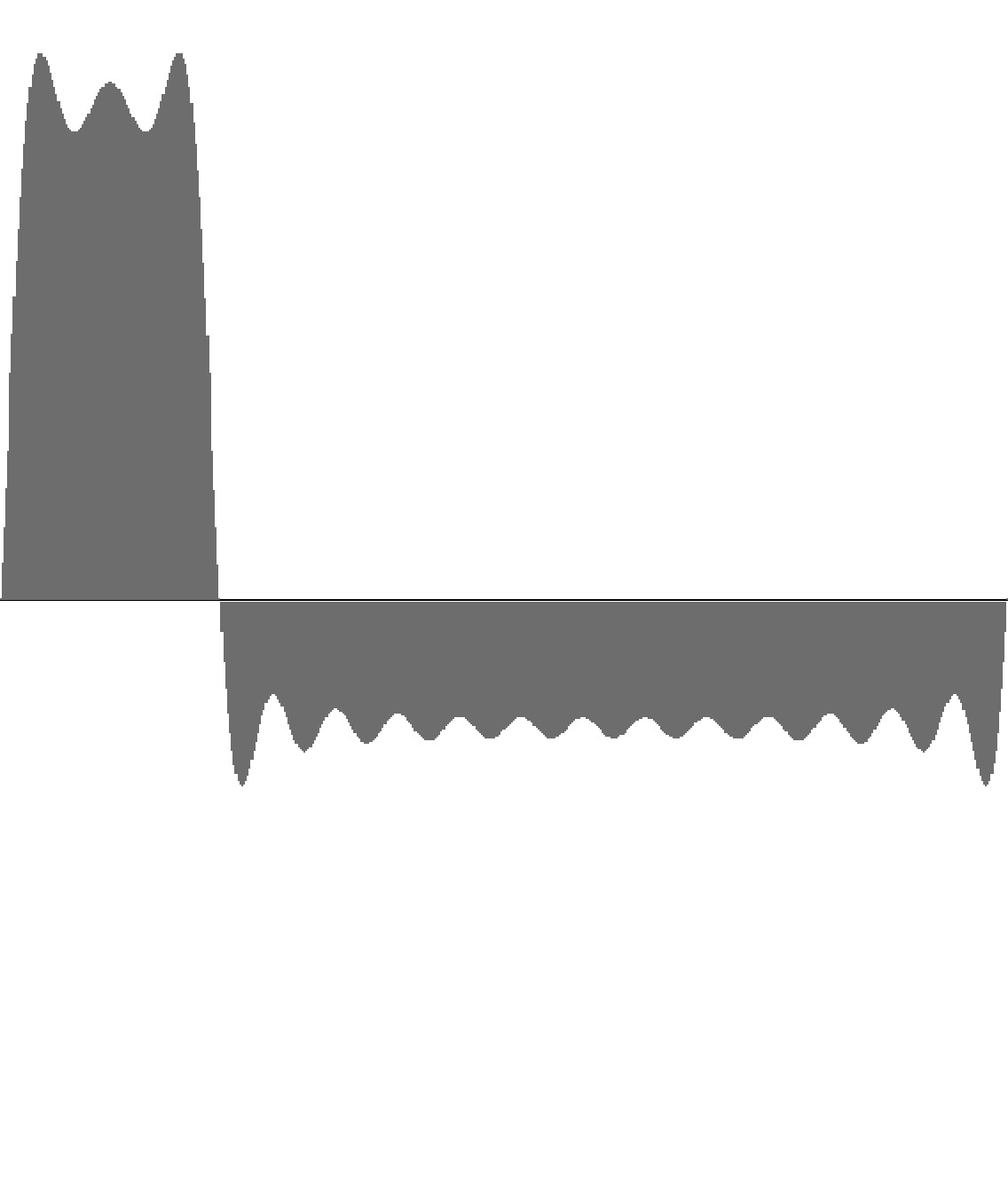
Figure 9-2: Rectangle wave with 16 harmonics and 20% duty factor. To hear a realization, click here.

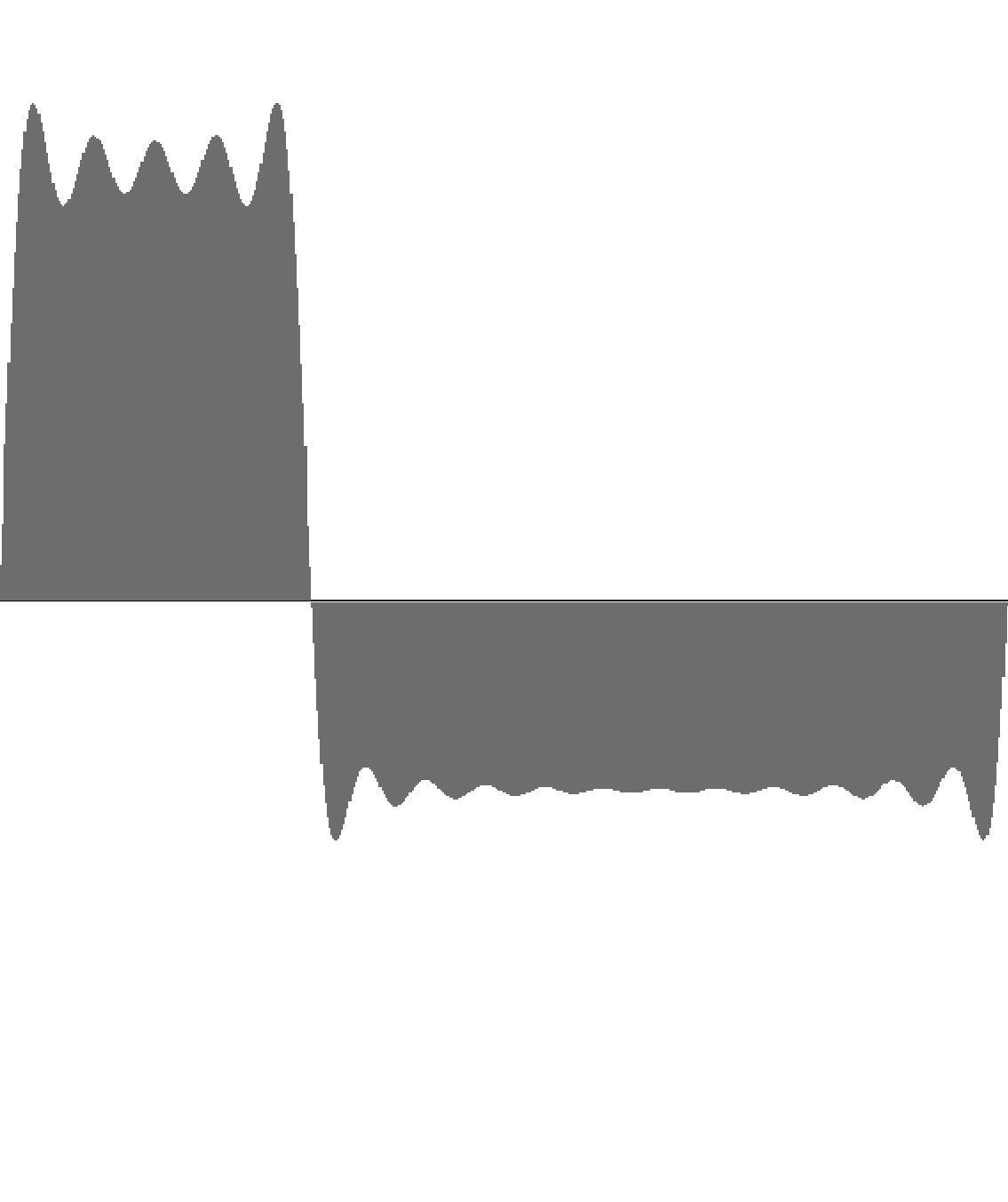
Figure 9-2: Rectangle wave with 16 harmonics and 30% duty factor. To hear a realization, click here.

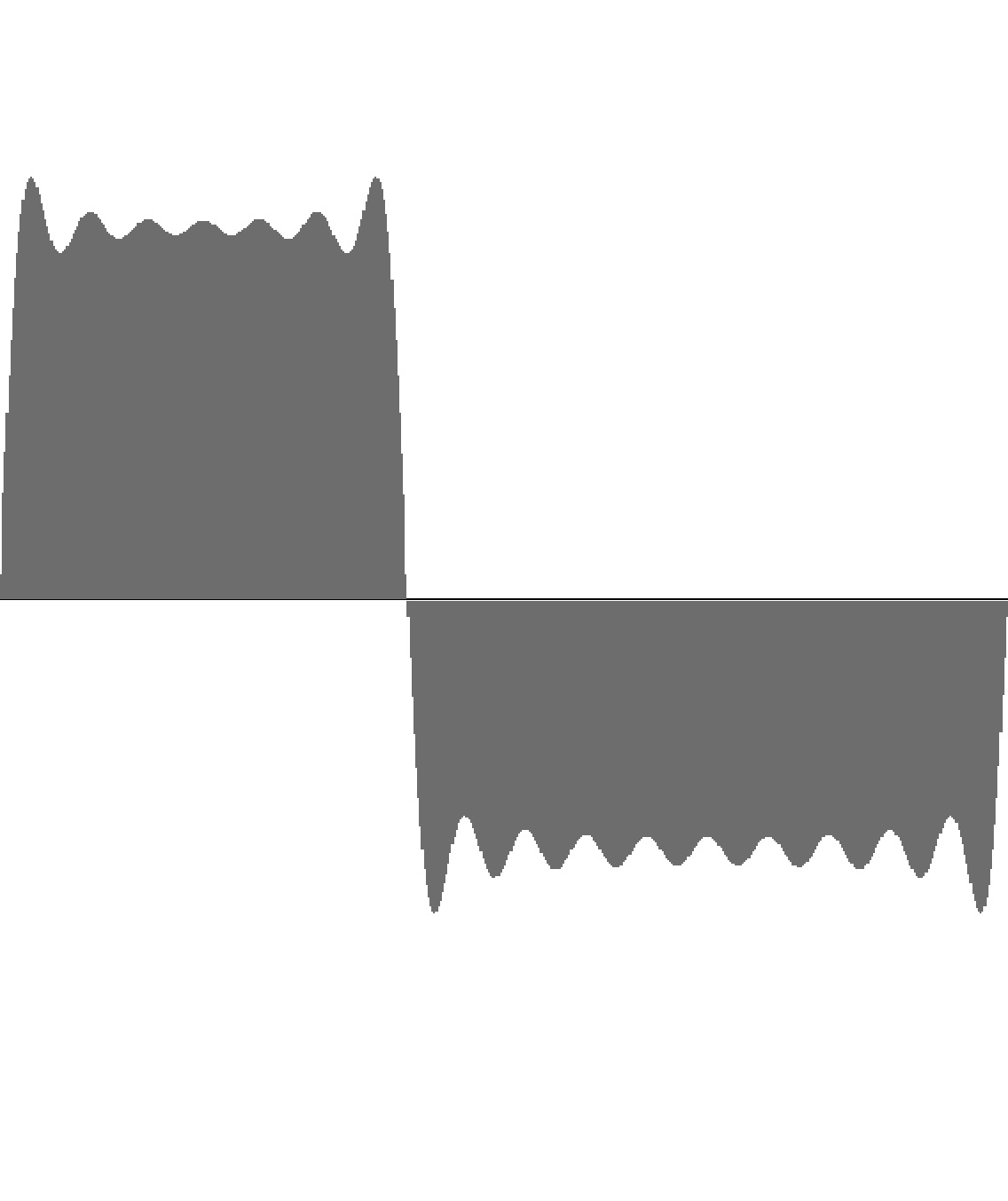
Figure 9-2: Rectangle wave with 16 harmonics and 40% duty factor. To hear a realization, click here.

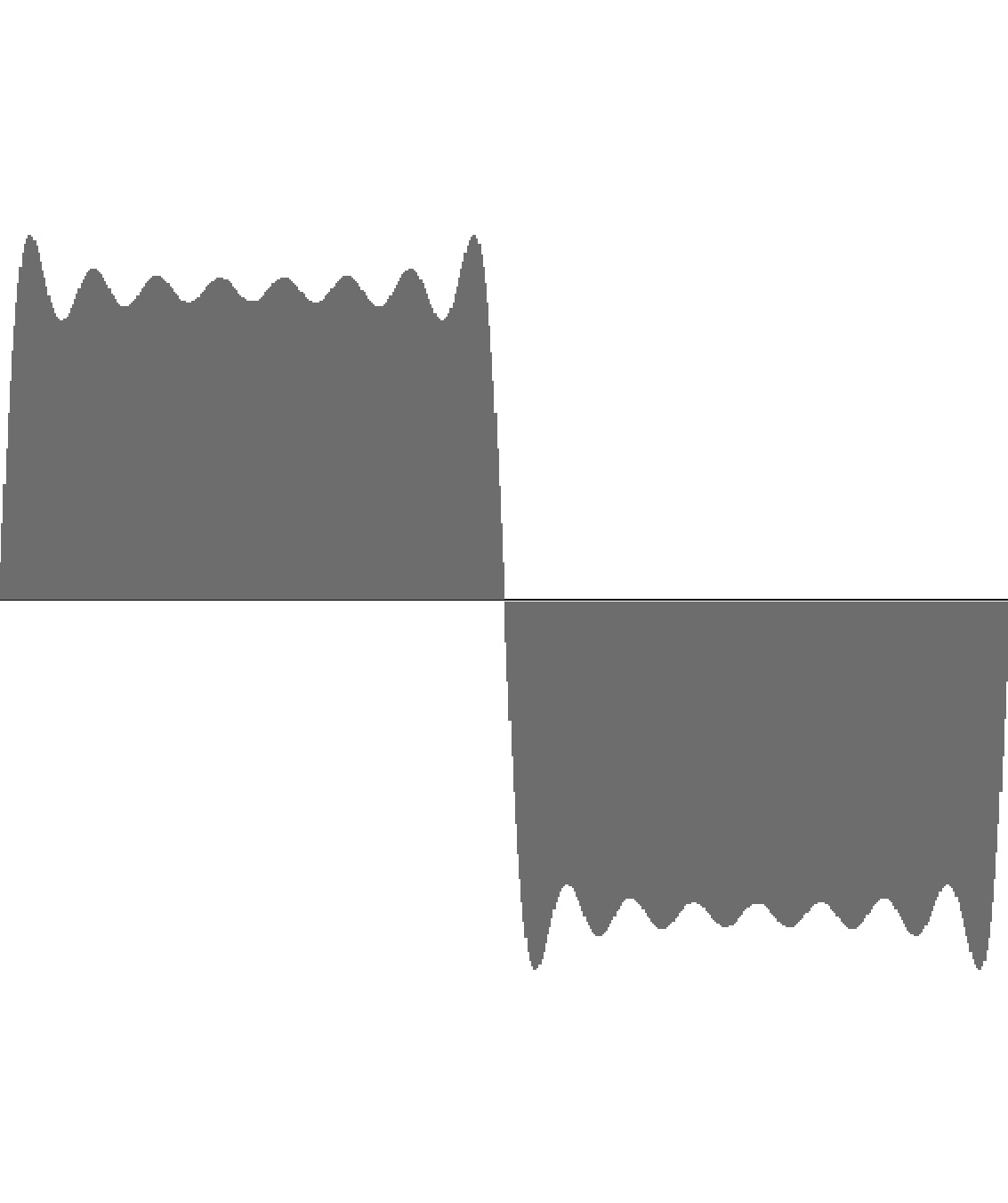
Figure 9-2: Rectangle wave with 16 harmonics and 50% duty factor. To hear a realization, click here.

Here is a tip about generating rectangle waves which I found on AllAboutCircuits.com and pass along unverified:

If n is the notional harmonic and D is the duty then if nxD is an integer the nth harmonic value is zero.

If D=0.25 then the 4th, 8th, 12th, etc... harmonics are zero.

If D=0.1 then the 10th, 20th, 30th etc are zero.

and so on.....

Low-Frequency Waves

In the classic waveforms presented up to this point, the harmonic with the greatest amplitude has generally been the fundamental. However with many low-frequency tones it is often desirable to shift the energy upwards in the frequency spectrum.

I have looked around for a mathematical formula that will do this, and the most suitable formula I have discovered is a discrete probably distribution — specifically the Negative Binomial distribution. Disregarding the distribution's original purpose¹, I have manipulated N and p to obtain instances which peak at specific harmonics while rolling off to around 0.001 at harmonic #16. The following table details N and p values for harmonics 1 (the fundamental) through 6.

Peak	Octave	N	p	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1	unison	1	0.375	1.000	0.625	0.391	0.244	0.153	0.095	0.060	0.037	0.023	0.015	0.009	0.006	0.004	0.002	0.001	0.001
2	1	2	0.469	0.941	1.000	0.797	0.564	0.375	0.239	0.148	0.090	0.054	0.032	0.019	0.011	0.006	0.004	0.002	0.001
3	1 ½	4	0.594	0.606	0.985	1.000	0.812	0.578	0.375	0.229	0.133	0.074	0.040	0.021	0.011	0.006	0.003	0.001	0.001
4	2	8	0.688	0.273	0.683	0.960	1.000	0.859	0.645	0.436	0.273	0.160	0.089	0.047	0.024	0.012	0.006	0.003	0.001
5	2 ¼	9	0.666	0.162	0.488	0.815	0.998	1.000	0.868	0.677	0.484	0.324	0.204	0.123	0.071	0.039	0.021	0.011	0.006
6	2 ½	19	0.782	0.060	0.250	0.545	0.832	0.997	1.000	0.872	0.679	0.481	0.315	0.192	0.110	0.060	0.031	0.016	0.007

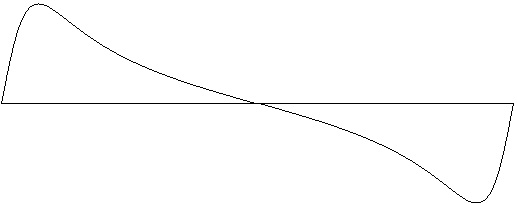
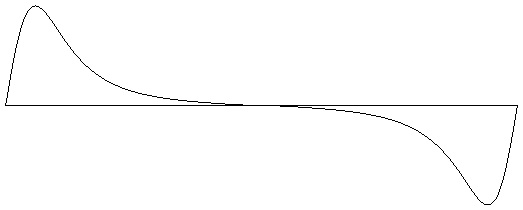
Figure 10-1: Waveform peaking on fundamental (unison). Generated using Negative Binomial formula with N=1 and p=0.375. Test ID: 801. To hear a realization, click here.	Figure 10-2: Waveform peaking on 2nd harmonic (1 octave). Generated using Negative Binomial formula with N=2 and p=0.469 Test ID: 802. To hear a realization, click here.
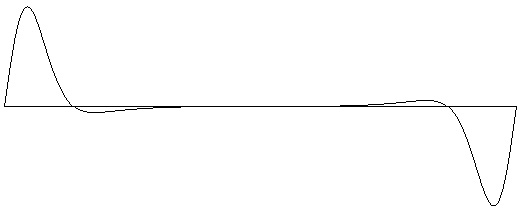
Figure 10-3: Waveform peaking on 3rd harmonic (1 ½ octaves). Generated using Negative Binomial formula with N=4 and p=0.594. Test ID: 803. To hear a realization, click here.	Figure 10-4: Waveform peaking on 4th harmonic (2 octaves). Generated using Negative Binomial formula with N=8 and p=0.688. Test ID: 804. To hear a realization, click here.
Figure 10-5: Waveform peaking on 5th harmonic (2 ¼ octaves). Generated using Negative Binomial formula with N=9 and p=0.666. Test ID: 805. To hear a realization, click here.	Figure 10-6: Waveform peaking on 6th harmonic (2 ½ octaves). Generated using Negative Binomial formula with N=19 and p=0.782. Test ID: 806. To hear a realization, click here.

Variations: Omit the even-numbered harmonics, multiples of 3, etc.

Octave-Doubled Sine Wave

In the octave-doubled sine family of waveforms, the only harmonic numbers present are powers of two; that is, octave doublings of the fundamental. The amplitudes all harmonics are the same.

To some this family of waveforms may seem trivial. I myself hadn't thought to include it when this page was originally posted. However I found it useful as a cheap way of extending one-octave sine clusters into multi-octave frequency ranges. In the process I rediscovered what many organ performers already know — that doubling a tone at the octave greatly increases its penetrating power.

Harmonic	1	2	4	8	16
Amplitude	1.000	1.000	1.000	1.000	1.000

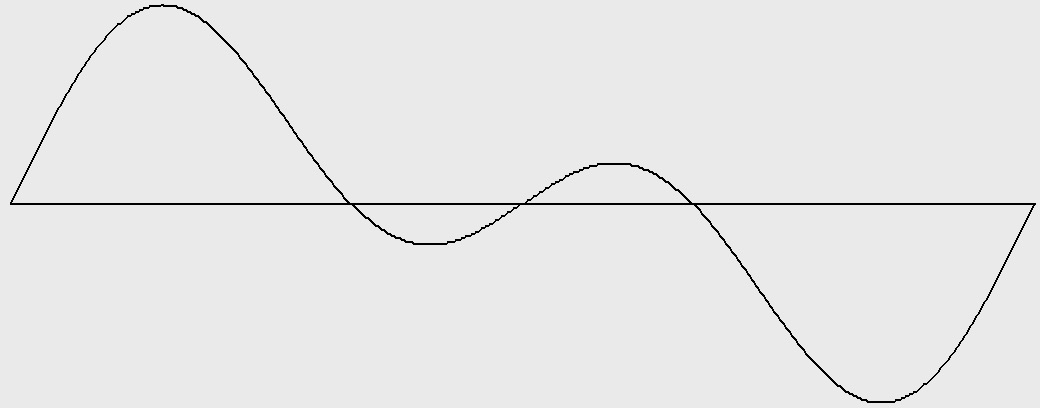
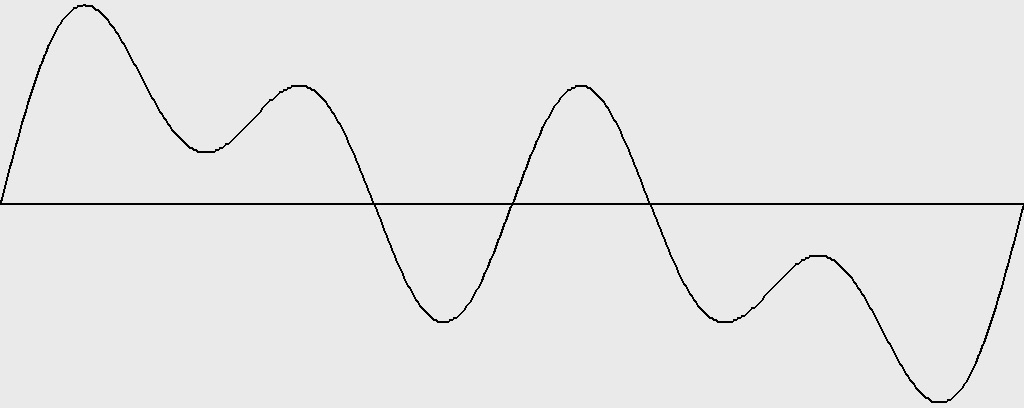
Figure 11-1: Octave-doubled sine wave with harmonics 1 and 2 (1 octave). Test ID: 902. To hear a realization, click here.	Figure 11-2: Octave-doubled sine wave with harmonics 1, 2, and 4 (2 octaves). Test ID: 904. To hear a realization, click here.
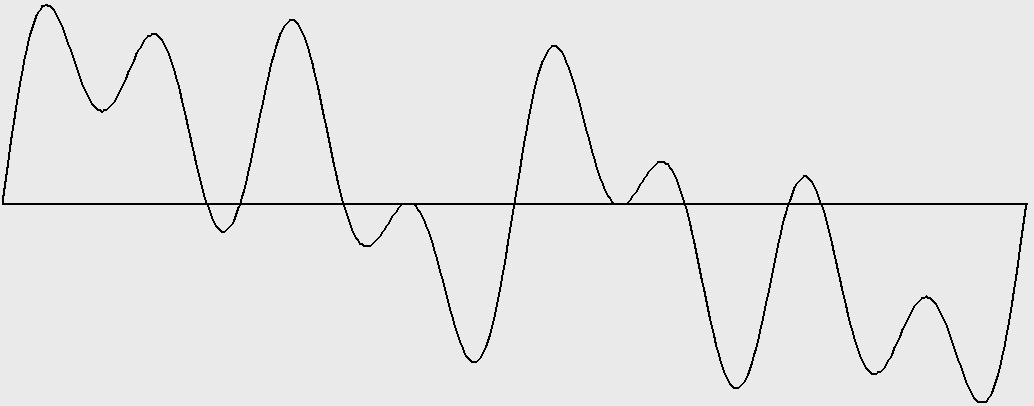
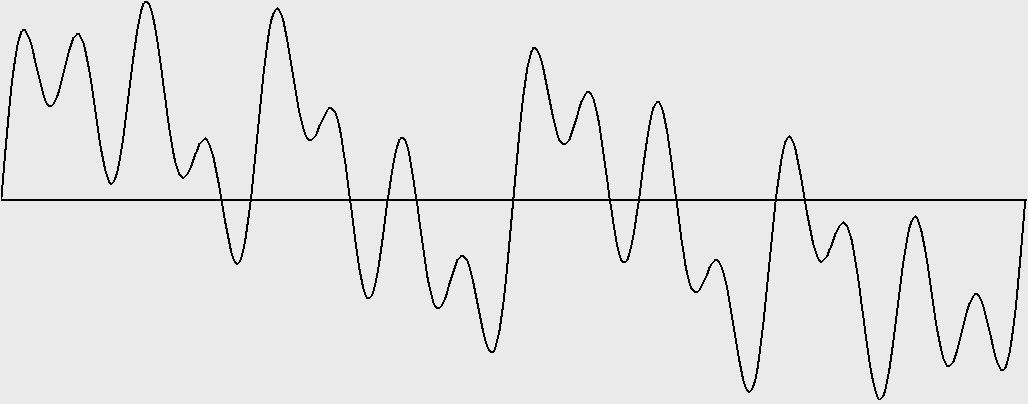
Figure 11-3: Octave-doubled sine wave with harmonics 1, 2, 4, and 8 (3 octaves). Test ID: 908 To hear a realization, click here.	Figure 11-4: Octave-doubled sine wave with harmonics 1, 2, 4, 8, and 16 (4 octaves). Test ID: 916. To hear a realization, click here.

Comments

For the record, this distribution predicts the number beyond N of random trials necessary to produce N successes if each trial has probability p of succeeding.

Page created: 2013-02-20

Last updated: 2017-06-24