Sine Waves
Introduction
Sine waves are the purest of tones. A sine wave has exactly one harmonic, which is the fundamental.
Sine waves are so-named because the air pressure at a specific instant of time can be calculated using the sine function. This function provides the basis for trigonometry, which Wikipedia defines as the “branch of mathematics which studies relationships involving lengths and angles of triangles.” Trigonometry was invented by Hipparchus of Rhodes sometime before 125 B.C., but most of what has survived comes to us by way of the geographer Claudius Ptolemy's Almagest. The Almagest was created around 150 A.D.1 It is notable for many things including a model of the heavens, including a map of the known world, including the concepts of latitude and longitude, and including a table of “chords” (a sine is a ‘half chord’). The precision of Ptolemy's table remained unsurpassed until the early modern era.
Measurement of Angles
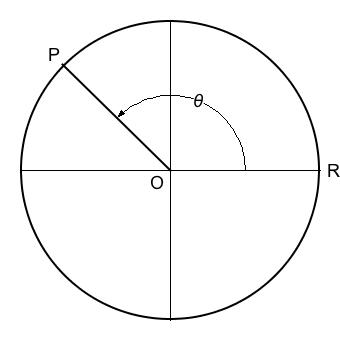
Sines being functions of angles, it is necessary first to understand how angles are measured. Construct a circle of radius 1, centered around the origin of a Cartesian coordinate system. Let O represent the origin, and let R represent the point where the positive x-axis intersects the circle. Now project a ray outward from the origin, whose angle in the counter-clockwise direction from the positive x-axis is given by θ. Let P represent the point where the ray intersects the circle. Figure 1 illustrates the construction just described.
Angles are commonly measured in three ways: turns, degrees, or radians.
The simplest and most obvious unit for measuring an angle is the full rotation or turn. A turn is also known as a cycle.
Degrees date back to the Babylonians and to the Greeks (e.g. Ptolemy). One degree divides a full rotation into 360 parts. This site favors degrees for measuring angles owing to their familiarity and convenience. If you're reading this text, you already know that a right angle measures 90°, that 45° divides a right angle in half, and that 30° divides a right angle into thirds.
Table 1: Turn/Degree/Radian equivalents for angle θ in Figure 1.
The standard unit for measuring angles is the radian, which in Figure 1 depicts as the circumferential distance from R to P. Radians leave a lot to be desired as a standard of measurement. What does one radian signify? The only thing familiar about them is that a full rotation measures out at 2π, which is the circumference of a unit circle. However, Wikipedia explains that mathematicians since Roger Cotes (d. 1716) have preferred radians to degrees because measuring angles in radians simplifies calculus. This is why the radian has been adopted by statute into the Metric System. It is also why the mathematical function libraries for programming languages such as C require angles to be expressed in radians.
Table 1 presents turn/degree/radian equivalents for eight positions of P around the unit circle in Figure 1. The position for 8/8 turns returns P to the same location it occupied for the zero angle.
An essential fact about angles is the fact that they ‘wrap-around’ upon themselves with each turn around the circle:
Here the triple-decker hyphen (≡) indicates equivalency: 0° and 360° both indicate the same point R in Figure 1; however, the first instance gets there immediately while the second only gets there after a complete turn.
What holds true for any θ holds true as well for 360°-θ, thus the meaning of a negative angle is formalized:
Sines from a Right Triangle
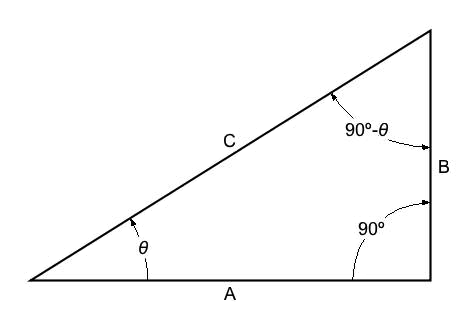
Educators traditionally explain the sine function with reference to a right triangle such as the one illustrated in Figure 2. Figure 2 orients the right angle at the lower right — any right triangle can be rotated into this orientation. Every triangle has, by definition, three edges and three vertices, which are the corners where edges intersect. Each vertex corresponds to an angle.
The triangle in Figure 2 has angle θ at the lower left vertex. The horizontal side of length A along the bottom is called the “adjacent” side. The vertical side of length B along the right is called the “opposite” side. The diagonal side of length C from lower left to upper right is called the “hypotenuse”.
Given the angle θ as shown in Figure 2 one calculates the sine of θ, notated sin(θ), by dividing the opposite length B by the hypotenuse length C:
| sin(θ) | ≡ |
|
Here the triple-decker hyphen (≡) indicates ‘is defined as’.
If you're familiar with sines, you're also familiar with cosines. As its name indicates, the cosine function is simply a complement to the sine. In particular, the cosine of the angle θ, notated cos(θ), is defined as the sine of the complementary angle (90° - θ). As Figure 2 illustrates, cos(θ) may be calculated by dividing the adjacent length A by the hypotenuse length C.
| cos(θ) | ≡ | sin(90° - θ) | ≡ |
|
Sines from the Unit Circle
The downside of explaining the sine function with reference to a right triangle such as Figure 2 is that the explanation becomes meaningless when θ ≤ 0° or θ ≥ 90°.
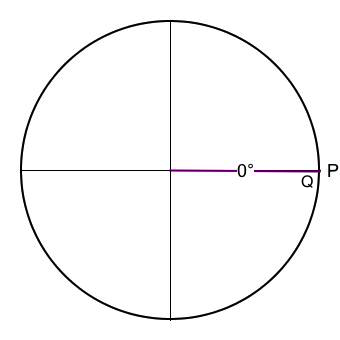
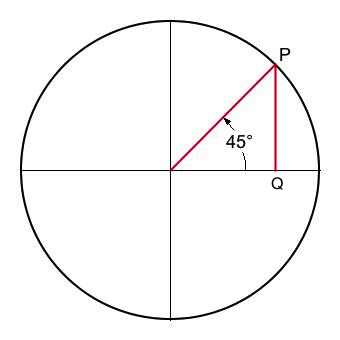
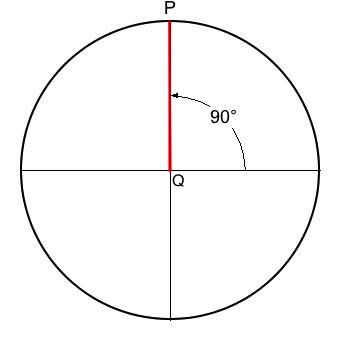
Here is a more general explanation which in fact closely resembles the explanation originally handed down by Ptolemy: Construct a circle of radius 1, centered around the origin of a Cartesian coordinate system. Now project a ray outward from the origin, whose angle with the positive x-axis is given by θ. Let P represent the point where the ray intersects the circle. Extend a vertical line from P until it intersects with the x-axis, and let Q represent the point of intersection. Then sin(θ) is defined as the vertical distance from P to Q.
Figure 3-1 through Figure 3-8 illustrate how unit-circle constructions may be used to derive sine values for angles ranging all the way around the circle from 0° to 360°.
| θ | Figure | Triangle Type | Edge Proportions | Sign | sin(θ) | |
|---|---|---|---|---|---|---|
| Adjacent | Opposite | |||||
| 0° | 2-1 | degenerate | 1 | 0 | 0 | |
| 45° | 2-2 | 45-45-90 | √2/2 | √2/2 | + | √2/2 |
| 90° | 2-3 | degenerate | 0 | 1 | + | 1 |
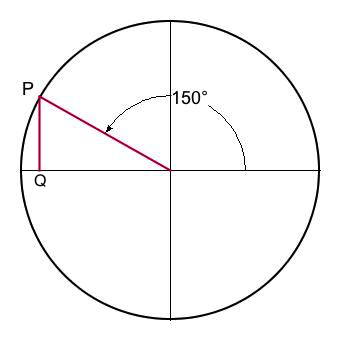
| 150° | 2-4 | 30-60-90 | √3/2 | 1/2 | + | 1/2 |
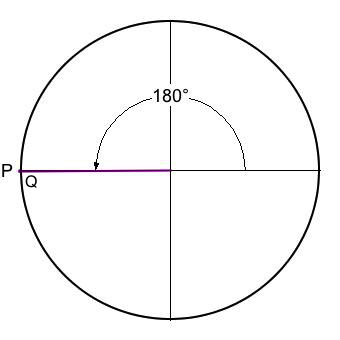
| 180° | 2-5 | degenerate | 1 | 0 | 0 | |
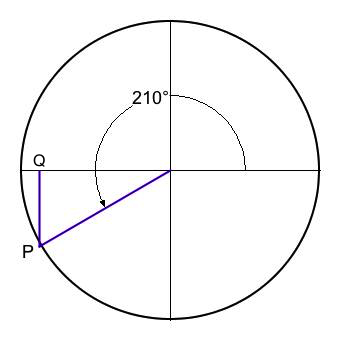
| 210° | 2-6 | 30-60-90 | √3/2 | 1/2 | - | -1/2 |
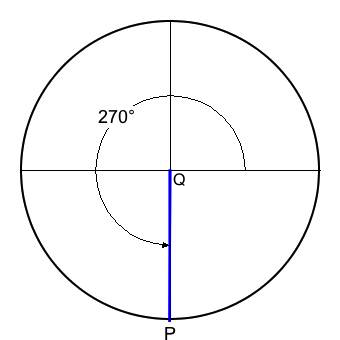
| 270° | 2-7 | degenerate | 0 | 1 | - | -1 |
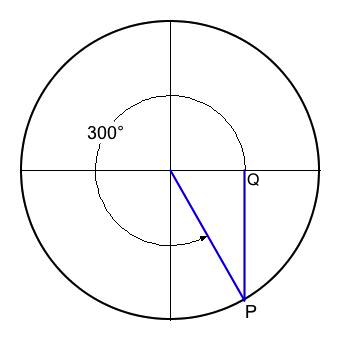
| 300° | 2-8 | 30-60-90 | 1/2 | √3/2 | - | -√3/2 |
Table 2: Sine calculations for Figure 3-1 through Figure 3-8.
The sine is a transcendental function, which means that one cannot generally calculate sin(θ) using a finite sequence of additions, of multiplications, and even of root extractions. Table 2 carries through the sine constructions in Figure 3-1 through Figure 3-8; these figures illustrate special circumstances either where the radius aligns directly with one of the coordinate axes or where a special right triangle is formed:
- For angles 0°, and 180° the x-intercept Q coincides with the radial terminus P. In these two specific instances P sits squarely upon the x-axis, so the sine is defined to be zero.
- For angles 90° and 270° the x-intercept Q coincides with the origin, so the distance from P to 1 is 1. The sine value will be +1 for 90° and -1 for 270°.
- For angles 45°, 150°, 210°, and 300° that the origin, the radial terminus P, and the x-intercept Q form right triangles with the adjacent edge extending from the origin to Q and the opposite edge extending from Q to P. Thus the sine magnitude is in each instance defined by the length of the opposite edge. The sine value will be positive when P is situated above the x-axis and negative when P is situated below the x-axis.
The first — and for a long time only — table of sines was the Table of Chords included in the Almagest. Understand that a chord is a straight line connecting two points on the unit circle, so that what we now know as a sine can alternatively be described as a half chord. Ptolemy's table and his methods for producing it are described in Wikipedia. Sine and cosine values can be readily calculated for the special angles of 30°, 45°, and 60°. Once these are obtained, intermediate values may be obtained through iterative applications of the compound angle formula.
and the half-angle formula:
| sin(α/2) | = | ± | √ |
|
Producing this table required a prodigious effort. It appears that “Ptolemy must have calculated chords to five sexigesimal [base 60] places in order to achieve the degree of accuracy …” found in the Table of Chords. No surprise that improved tables would not appear until the late 16th century.
Sound Waves
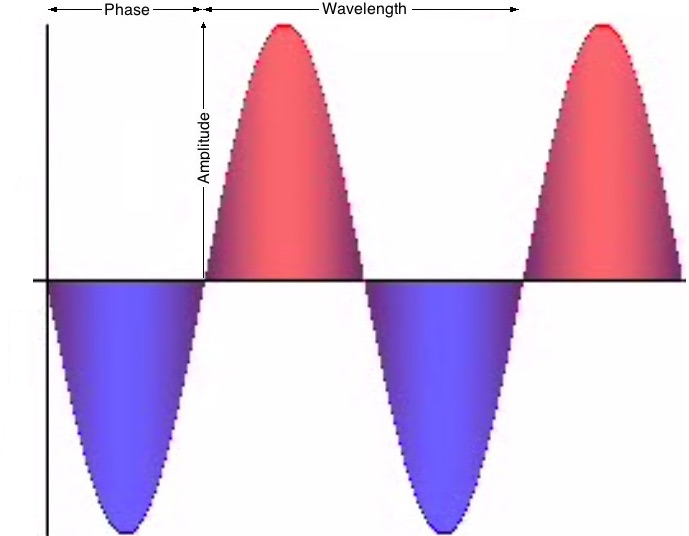
The graph shown in Figure 4 plots the values of the equation:
| y(t) | = A·sin | [ | 360° | ( |
|
+ φ | )] |
where
- y(t) indicates the momentary intensity of the sound wave at time t.
- A indicates the amplitude, (or more specifically the peak amplitude) which determines how loud the sound will be.
- ν indicates the wavelength expressed as the fraction of seconds required to express one cycle.
- φ indicates the phase, which expresses how the waveform aligns with time 0. For example if the wavelength is 1/440 seconds then a phase of 0.25/440 will align the peak of the waveform with time 0.
A fourth property of the sine graph is the frequency ω, which is inversely proportional to the wavelength:
| ω | = |
|
The frequency is what you get by counting how many wave cycles occur during a unit of time, and the proportionality constant c in the above equation is the speed of sound, 767 mph. Thus a frequency of 440 Hz. (440 cycles per second) has a wavelength:
|
= |
|
= |
|
× |
|
× |
|
= |
|
= 1125 feet per cycle. |
Frequency corresponds to pitch in this way: Doubling the frequency raises the pitch by one octave.
A sine wave, strictly speaking, has a constant phase offset φ of zero. If the phase offset is 90° then what you have, again strictly speaking, is a cosine wave. However under most circumstances phase is not perceptible to the human ear, so people generally just talk about sine waves. You can also use the word sinusoid for any oscillating curve that could be phase-shifted to make a sine wave.
A graph like the one shown in Figure 4 appears in the original (1687) edition of Isaac Newton's Principia. It is certain that Newton was fully aware how closely its oscillations resemble simple waves such as the ups and downs of ripples on a pond. Beyond that, he develops the theory of a harmonic oscillator as a mechanism for producing sinusoidal waves.
According to Wikipedia, the understanding of sound waves as a mechanism for propagating energy through air appears in Book V of his De architectura (The Ten Books of Architecture) by Vitruvius, a Roman. This treatise dates back as early as 20 B.C., predating even the Almagest. Wikipedia continues:
… Vitruvius describes sound as a wave comparable to a water wave extended to three dimensions, which, when interrupted by obstructions, would flow back and break up following waves.
The opening sentence of this page asserts that sine waves are the “purest” of all waveforms. Here are four arguments in support of this assertion:
- The first argument for purity is sound quality. Click on the links provided to compare a sine wave with a triangle wave, a rounded sawtooth wave, a square wave, a sawtooth wave, and a pulse wave.
- The second argument for purity is the simplicity of the waveform. Consider Figure 4. The waveform proceeds from the bottom of a trough to the top of a peak, then back again, with no digressions along the way. It does so without discontinuities and without sharp edges. The slope of the sine function itself oscillates sinusoidally between a positive maximum, where the original function ascends through the t-axis, and a negative minimum, where the original function descends through the same axis.
- The third argument for purity is the fact that the simplest mechanical oscillators undergo sinusoidal trajectories. One of the earliest mechanisms for simple harmonic motion was a weight dangling from a spring; this was investigated by Robert Hooke and Christiaan Huygens during the 1670's.
- The fourth argument for purity is the 1742 discovery that every periodic waveform can be resolved into “simple modes”, which are in fact sinusoidal waves. This discovery seems due to Daniel Bernoulli during investigations into vibrating “bands”, among whose oscillations Bernoulli had “often perceived three or four sounds at the same time”.2 In fact the frequencies of these sinusoids have the proportions 1, 2, 3, 4, and so forth. This sequence has come to be known as the overtone series, or alternatively the harmonic series.
This page completes with a video which sweeps a radius around a unit circle and graphs the sine values thus produced. The video animates a diagram by Hermann Helmholtz. Helmholtz originally contrived this diagram to explain how successive sine constructions can be plotted to produce an oscillating curve.3
The video has two graphic components. At the far left is a circle with x and y axes, which serves in the manner of Figure 3-1 through Figure 3-8. The remainder of the graphic is an intensity/time graph, which will come to resemble Figure 4. During each frame of the video, the vertical distance from the x-axis to the point where the radius intersects the circle is taken as the momentary intensity. The intensity/time graph scrolls rightward by one pixel; then the new intensity value is plotted in the leftmost position.
The demonstration proceeds in four phases, each lasting 3 seconds. Each phase populates 250 consecutive pixels on the intensity/time graph. Each phase is distinguished by a particular sweep rate, that is, the number of degrees by which the radius advances each time a new sine value is calculated. In the audio accompanient, a phase is accompanied by a sine tone whose frequency is proportional to the sweep rate:
- The radius cycles twice around the circle using a sweep rate of 2 × 360° / 250 = 2.88° per frame. This first phase is accompanied by a 110 Hz. sine tone.
- The radius cycles four times around the circle using a sweep rate of 5.76° per frame. The accompanying sine tone ascends to 220 Hz.
- The radius cycles sixteen times around the circle using a sweep rate of 23.04° per frame. The accompanying sine tone ascends to 880 Hz.
- The radius cycles eight times around the circle using a sweep rate of 11.52° per frame. The accompanying sine tone descends to 440 Hz.
Video 1: Sine waveforms generated by sweeping a radius around a circle.
Comments
- My historical source for ancient trigonomitry is Morris Kline's Mathematical Thought from Ancient to Modern Times (Oxford University Press, 1972), volume 1, page 119.
- The best historical source I could find for sinusoidal waves was the Groves entry, Physics of music by various authors. Another source was a powerpoint presentation, “Waves, History and Applications” from the Basque Center for Applied Mathematics.
- On the Sensations of Tone, page 21, Figure 7.
| © Charles Ames | Page created: 2013-02-20 | Last updated: 2017-06-24 |