Complementary Rhythm Generator
Backstory
Coming into this attraction, it helps to understand three things. First, you should know something about my technique of statistical feedback, which promotes balance among resources. The workings of this technique are explored in the Statistical Feedback attraction. Second, you should understand the components of an AI decision engine. The basic features of such an engine are demonstrated in the Intelligent Part Writer attraction. Third, you should understand how meter arises.
Introductory music theory courses generally teach about tonality without talking about rhythm. I think that is wrong. You can't understand tonality without knowing about cadences and you can't understand cadences without knowing what a down beat is.
Introductory music appreciation courses, by contrast, will teach you that meter is a framework of strong and weak accents, within which the rhythm unfolds. That's at least a start. Appreciation courses may also teach you that recurring meter, such as the meter in Baroque dance music, sets up expectations which composers can play against using devices such as syncopation and hemiola. Such a course may even get to the changing time signatures of Igor Stravinsky; that is, to non-recurring meter. But how do metric patterns arise in the first place? Are they somehow just brought into being through the imposition of a time signature? Do performers make meter happen by stressing down beats?
My own awareness that rhythm was more than just ways of dividing time came during undergraduate composition lessons with Karl Kohn at Pomona College. Kohn's repeated comment was this: “Get off the down beat.” Such instruction was accompanied in one instance by Kohn's suggestion to insert an on-beat rest at the beginning of a phrase. By reintroducing me to the notion of a pick-up rhythm, Kohn showed me that there is a functional difference between a down beat and an up beat. This brought me to the theoretical question: What distinguishes a down beat from an up beat? Which comes back to the question asked just previously.
There is a straightforward answer to the question: What makes meter? The answer is apparent in most every metric score ever written, especially in scores of dance music. But for me this answer had to be laid out plainly, and this happened during a semester abroad at Oxford, where I was satisfying the music department's medieval history requirement.
Consider first the stratified rhythms illustrated by Figure 1.
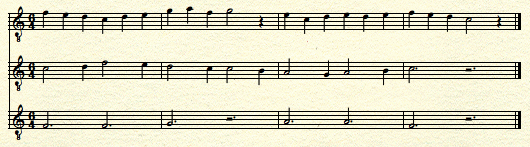
Figure 1: Motet from the school of Notre Dame, probably by Pérotin, composed around 1250. Reproduced from Gustave Reese, Music in the Middle Ages, Ex. 91.
MIDI Rendition of Figure 1.
Figure 1 presents one of history's earliest notated examples of meter. The passage employs a stratified style of fast-moving notes, slower notes, and single long notes (the tenor). The time signature is an artifact of Gustave Reese's transcription — time signatures weren't actually invented until some fifty years later. Yet the stratified motion of parts creates a tiered scheme of accentuation, and this scheme is consistent with Reese's choice.
The stratified style attributed to Pérotin is the simplest way of realizing a meter. For a more generalized principle, we need to skip forward to Guillaume de Machaut, and specifically to his collection of motets. According to Gustave Reese, Machaut numbered the motets himself; thus we are privileged with witnessing how Machaut's rhythmic style evolved.
- The earliest of Machaut's motets take up the stratified style from Pérotin.
- As the sequence of motets progresses, activity starts trading off between the descant parts.
- One also encounters rest in their most primitive form as off-beat hockets.
- Later, parts begin to syncopate and true pick-up figures appear.
- In the latest motets, Machaut goes to town with syncopation.
The principle at work in all but Machaut's most syncopated later motets is this: meter becomes manifest through the convergence of parts on stronger beats and the divergence of parts on weaker beats. Taken in isolation, an individual part can project the beat by favoring on-beat notes over off-beat notes. However the full expression of meter only comes about through the interaction of parts. The parts complement one another. If one part avoids the down beat, most other parts embrace said down beat. If one part embraces an off beat, most other parts avoid said off beat.
The fact that Machut's later motets relax this principle reflects less the principle's validity than on the fact that Machaut was not writing dance music.
The Stream/Pulse Grid
Table 1 correlates the rhythm of Figure 1 with the meter inferred by Reese. To achieve this correlation, it is necessary to divide notes into atomic Events. Dividing thus produces a grid whose cells are Events, whose rows are Streams, and whose columns are Pulses.
Pulse # 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 Duration Q Q Q Q Q Q Q Q Q H Q Q Q Q Q Q Q Q Q Q H Q Beat Type 3 1 2 3 1 2 3 1 2 3 2 3 1 2 3 1 2 3 1 2 3 2 Descant #1 Descant #2 Tenor
Table 1: Event analysis of Figure 1.attack;
tie;
rest.
Notice that each Pulse in Table 1 is associated with a Beat Type. The Beat Type indicates whether the pulse is a down-beat (3), an up-beat (2), or an off-beat (1).
Notice also the change of jargon: I henceforth use the word Stream in place of “part” because parts are technically associated with players and players of polyphonic instruments can potentially handle more than one stream.
The idea of representing musical events as cells of a grid, is ubiquitous; for example, in the “piano-roll notation” used by MIDI sequencing software. The idea that such a grid could provide the substrate for a generative process that actively coordinated stream events took several AHA experiences.
The most basic insight was recognizing balance as a driving force in ensemble interaction. It's as if the composer is thinking: “The tenor and soprano have played before; now I'll let the alto take its turn. I first worked on this problem in connection with Cybernetic Composer's ragtime emulation, where I managed to generate some four-part textures with complementary lines. In the end I opted for a single melodic line over an oom-pah accompaniment, limiting balance to coordinating ooms and pahs.
The next hurdle was generalizing the method to handle not just attacks, but also rests and ties. Here came the insight that the process needed to operate on a level more granular than the note — hence the stream/pulse grid. At each grid point, weights controlled the balance of attacks, ties, and rests. I emphasize that this process was never a random; rather it employed statistical feedback to actively promote balances.
This is where things stood when for various reasons I walked away from computer music for twenty years. In 2011 I began working on several new compositions, in the process building up new software frameworks to share functionality from one project to the next. Each new composition took an increasingly elaborate approach to generating complementary rhythms. Among other things, the alliances between streams became increasingly fluid. So where initially I would allow a certain set of weights to control a entire passage, in the later pieces the lead would pass from one stream to another, or the texture would alternate between complementary rhythms and concerted rhythms. Hence the ability to implement “meta” decisions.
Applet Components
The Complementary Rhythm Generator applet reads in an XML data file with the object hierarchy shown in Figure 2. Of these objects, Stream and Pulse respectively define the rows and columns of a stream/pulse grid. Each Pulse references a Beat Type. The goal of the applet, or more precisely of its first stage, is to select an Event Type for each cell of the grid (i.e. each event). Instructions for doing this are provided by the Grammars, which themselves have a complex object hierarchy (not shown). Once the stream/pulse grid has been elaborated into notes, a second stage selects a Sounds notes. Although Sounds are specific to Streams, each Sound references a Chroma. Chromas enable the sound-selection engine to balance resources shared between Streams.
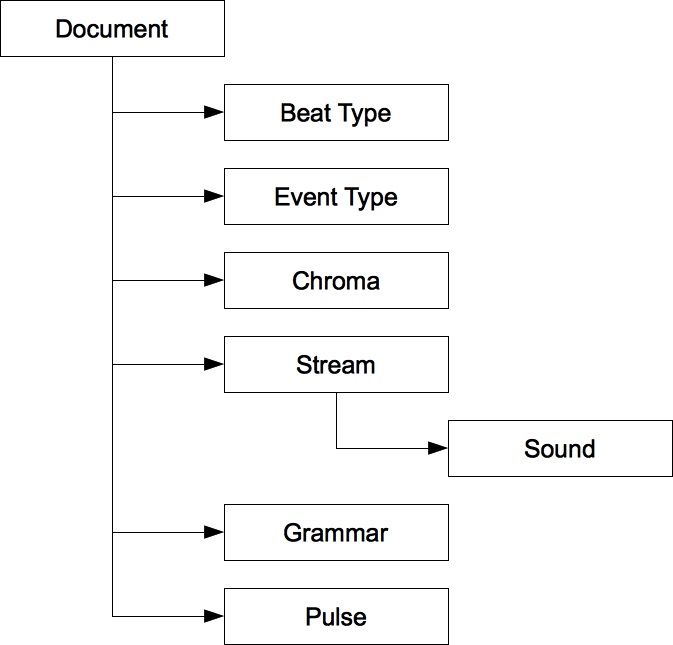
Figure 2: Object hierarchy for Complementary Rhythm Generator documents.
Beat Types
A Beat Type identifies the role that a Pulse serves within the measure. Each Beat Type has four attributes: ID, Name, Description, and Level. All of the scenarios presented in this attraction employ the set of beat types enumerated in Table 2.
ID Name Description Level 0 16 Other Sixteenth 0 1 16* Initial Sixteenth 0 2 8 Other Eighth 1 3 8* Initial Eighth 1 4 Q Quarter 2 5 M Measure 3
Table 2: Beat Types used in this presentation.
The Level is a legacy attribute indicating the precedence of the pulse in the scheme of accentuation. All other attributes are simply alternative ways of naming the thing. Notice there are two flavors of sixteenth-note offbeat: initial and other; likewise there are two flavors of eighth-note offbeat. Most of my prepared scenarios draw no distinction between flavors; however, Scenario #5 divides measures asymmetrically between an eighth-note phrase-completion portion and a dotted-quarter phrase-initiation portion.
Pulses
The metric framework shown in Table 3 will be shared by all six scenarios. The framework contains four 2/4 content measures capped by a 1/4 cadence measure. There are eight sixteenth-note pulses in each content measure and one half-note pulse in the cadence measure.
Measure: 1 2 3 4 5 Pulse ID: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 Duration: S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S S H Beat Type: M 16* 8* 16 Q 16* 8 16 M 16* 8* 16 Q 16* 8 16 M 16* 8* 16 Q 16* 8 16 M 16* 8* 16 Q 16* 8 16 M
Table 3: Metric framework for all prepared scenarios in this attraction. Beat types are explained in Table 2.
Event Types
An Event Type defines how a Stream will behave within a specific Pulse. Each Event Type has seven attributes: ID, Name, Description, Color, Category, Default for Category, and Bias. Event Types also have optional collections of Source Beat Types and Target Beat Types. Table 4 lists three basic Event Types.
ID Name Description Icon Category Default Bias 0 - Rest REST true NONE 1 & Tie TIE true TRAILER 2 A Attack ATTACK true NONE
Table 4: Basic Event Types used in this presentation.
The ID, Name, Description, and Color attributes are alternative ways of identifying an event type. There are three event-type categories:
- REST — The Event contains no sound.
- TIE — The Event continues the note from the same Stream in the previous Pulse.
- ATTACK — The Event initiates a new note.
These descriptions are sufficient to generate all note start times and durations, once the cells of a stream/pulse grid have been filled in with Event Types. The list of event types must represent each category at least once. Every category must have exactly one Default for Category instance.
There are five Bias options.
- NONE — No restrictions.
- LEADER — The current note may not be followed by a rest (or end-of-stream).
- TRAILER — The current event may not be preceded by a rest. Event Types of the TIE category must always have the TRAILER bias.
- BOTH — The current note may not be either preceded or followed by a rest.
- EITHER — The current note may be preceded by a rest or followed by a rest, but not both.
Now to explain the Source Beat Types and Target Beat Types collections. These collections are relevent to Event Types of the ATTACK category. By default, an Event Type can begin on any Beat Type and end prior to any Beat Type. If the Source Beat Types collection has any members, then the Event Type may only be used on a Pulse whose beat type is a member of the Source Beat Types collection. If the Target Beat Types collection has any members, then notes initiated with this Event Type must terminate just prior to any Pulse whose beat type is a member of the Target Beat Types collection. So for example, Scenario #5 employs an Event Types which only begins on a “Measure” and only ends prior to an “Initial Eighth”.
Grammars
Generative grammars are associated Noam Chomsky. A generative grammar is a set of directions, variously called productions or rewrite rules, which can elaborate a cursory description of an entity into a detailed description of its components.
Within the Complementary Rhythm Generator applet, a Grammar starts with an Event and applies productions to deduce which Event Types should be considered for that Event. Thus given a certain combination of a Stream, a Beat Type, and, sometimes, a meta-decision context (explained elsewhere), the Grammar will enumerate a list of Event Types. Taking this mission a step further, each production specifies not just an Event-Type, but also an associated weight. Understand that these weights do NOT determine the order of preference — at least not directly. Rather the weights influence the Event Type's relative frequency of usage, over time, within the indicated Stream.
Stream Beat-Type ID Beat-Type Name Event Type Weight All 0 16 Tie 1 1 16* Tie 1 2 8 Tie 1 3 8* Tie 1 4 Q Tie 1 5 M Attack 1
Table 5: Cadence Grammar for all scenarios. Each row in this table describes a production. The Stream and Beat Level columns identify conditions which must all be satisfied for the production to apply. The Weight identifies how much the nominated Event Type should be used, relative to other Event Types satisfying the same conditions.
A simple example is provided by Table 5, which all six scenarios use to handle the cadence pulse.
This Grammar applies the same logic to all Streams: If the Beat Type, is “M” (“Measure”)
then initiate an attack ( ); otherwise, tie over from the preceding Event (
); otherwise, tie over from the preceding Event ( ).
).
My appropriation of Chomskian jargon is consistent with the explanation of grammars given above, but it goes no farther. For Chomsky, every statement properly generated using a grammar's rewrite rules is a “competent” statement. In my own framework, grammars simply propose; competence is enforced by the AI search engine. For example it is not competent to follow a rest with a tie, yet ties may be among the resources that the application is trying to keep in balance. So the grammar goes ahead and proposes a tie. The search engine rejects that option, but also understands that it should strive harder to employ ties in the future.
Grammars have other features. You can organize Streams into groups and implement meta decisions. Meta decisions can influence both how groups of streams interact and how individual streams behave over designated periods. Meta decisions can be nested to any level. You can, perhaps as a consequence of a meta decision, direct one stream to imitate another stream rhythmically.
Chromas
My usage of the word “chroma” follows that of James Tenney in Meta+Hodos. The Chroma serves in the sound-selection pass to identify resources that should be maintained in balance. Typically if you're working with pitched sounds, you'll want pitches of like chromatic number to share the same Chroma. If you're working with unpitched sounds like drums and cymbals, you'll want each sound to reference a different Chroma. Chromas have two attributes: an ID and a Weight.. The weight influences how much Sounds referencing this chroma should be used relative to the other Sounds available to a Stream.
Streams and Sounds
Each of the six scenarios presented in this attraction has four streams. The attributes given to these streams vary from scenario to scenario. Streams have five attributes: ID, Name, Percussion flag, MIDI Program (relevant only when Percussion is false), and MIDI Velocity.
Every Stream instance contains one or more Sounds. Sounds have three attributes: ID, Chroma, and MIDI Key.
Decision Engines
The Complementary Rhythm Generator applet employs two decision engines. These engines execute sequentially: An event engine generates notes, while a sound engine selects sounds for notes. The event engine leverages actual mechanisms from my compositional framework, and its execution is animated. The sound engine is perfunctory and executes without animation.
Event Engine
Expressed in the jargon of my production framework, the event engine stands as the first of two stages. This first stage handles a single problem, which is to select Event Types for a Stream/Pulse grid. The event engine is implemented using a “Heuristic Search” strategy, with simple backtracking. The Events within each Pulse stand as decisions, the options of which are Event Types. Pulses are processed in time order, advancing from left to right unless an impasse is reached. Within a Pulse, the order by which Events are considered is dynamic.
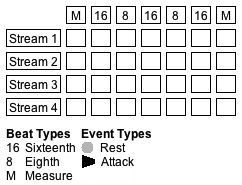
Figure 3: Example Stream/Pulse grid.
To understand how the event engine works, we will walk through an example using the Grammar detailed in Table 6 to populate the grid shown in Figure 3.
Stream Beat-Type Event Type Weight All 16 Attack 0.29 (2/7) 16 Rest 0.71 (5/7) 8 Attack 0.57 (4/7) 8 Rest 0.43 (3/7) M Attack 0.86 (6/7) M Rest 0.14 (1/7)
Table 6: A simple Grammar to nominate Event Types .
Productions
First to the productions which nominate Event Types for grid cells (Events). The event engine invokes productions that is, each time the engine advances into an Event. Productions are dynamic in this sense: if after backtracking the engine advances into an Event that it visited previously, a new set of Event Types are nominated. This allows the engine to adapt productions to changing contexts (see Scenario #3). However since the present walk-through does not employ contexts, the Grammar in Table 6 responds solely to Stream and Beat Type. Productions therefore behave as if they were static:
- Events in Pulses with Beat Type “16” (2, 4, 6) will always map to productions 1 and 2.
- Events in Pulses with Beat Type “8” (3 and 5) will always map to productions 3 and 4.
- Events in Pulses with Beat Type “M” (1 and 7) will always map to productions 5 and 6.
Constraints
Here is the “Heuristic Search” decision strategy in a nutshell: Having invoked its Grammar to nominate Event Type options for a grid cell, the event engine sorts these options into preference order (see below), then proceeds to consider each option. This is where constraints come into play. If an option satisfies all constraints, the engine advances to the next grid cell. If an option fails to satisfy any constraint, the option is rejected and the next option is taken up. When none of the options are satisfactory, the engine backtracks to the previous grid cell and takes up that cell's next option.
For this walk-through, the only relevent constraints are the limits controlling how many simultaneous attacks may occur during a given Pulse. These limits are determined by summing weights for Event Types of the ATTACK category, by rounding down for the lower limit, and by rounding up for the upper limit. For example, the attack weight for all streams in Pulse #1 is 0.86. Therefore the number of attacks which should occur during Pulse #1 is 4 times 0.86, or 3.43. The event engine therefore constrains the choices for Pulse #1 so that the total number of attacks must be at least 3 and at most 4.
Pulse # Beat Type Attack Weight Average Attacks Lower Limit Upper Limit 1 M 0.86 3.43 3 4 2 16 0.29 1.14 1 2 3 8 0.43 2.29 2 3 4 16 0.29 1.14 1 2 5 8 0.43 2.29 2 3 6 16 0.29 1.14 1 2 7 M 0.86 3.43 3 4
Table 7: Attack weights; lower and upper attack-count limits for the grid shown in Figure 3, based on the productions listed in Table 6.
Table 7 applies the previous paragraph's calculation to all seven of the Pulses depicted in Figure 3. There are 2,500,000 grid solutions that satisfy the limits indicated in Table 7, but not all these solutions are of the same quality. In addition to satisfying these lower and upper limits, we also want the intra-stream balances between rests and attacks to conform, roughly, to the indicated weights. One test of conformity would be to verify that the total number of attacks for any Stream be around:
Now since my approach constrains the numbers of attacks used in each Pulse, I might similarly have constrained the number of attacks in a Stream. Had I done so, the engine would face situations where it has nearly completed a grid (normally with many more than 7 pulses), only to discover that the attack count is off. Too many attacks overall would cause the engine mostly to change attacks near the end of the stream to rests. Too many rests overall would cause the engine to end the stream with a preponderance of attacks.
Decision-Level Heuristics
This is where decision-level heuristics come to the rescue, along with my favorite heuristic method, statistical feedback. You may remember that my nutshell description of the “Heuristic Search” strategy deferred explanation of sorting options by “preference”. Well here we are.
Instead of waiting until the end to fix things up, a selection
engine driven by statistical feedback strives to maintain balances from moment to moment.
Table 8 continues our walk-through by tracing how statistical feedback strives to balance “Attack” ( )
and “Rest” (
)
and “Rest” ( ) Event Types.
The trace is simplified because it considers only one Stream.
It also leaves out aside two features which the application in fact uses: normalization and random leavening.
(Both of these features are explained in “Statistics and Compositional Balance”.)
The trace is hypothetical because it assumes that the Event Types favored statistically are the ones actually selected.
In actual practice the selections will be constrained by lower and upper attack limits, as previously described.
) Event Types.
The trace is simplified because it considers only one Stream.
It also leaves out aside two features which the application in fact uses: normalization and random leavening.
(Both of these features are explained in “Statistics and Compositional Balance”.)
The trace is hypothetical because it assumes that the Event Types favored statistically are the ones actually selected.
In actual practice the selections will be constrained by lower and upper attack limits, as previously described.
Attack Rest Favored Pulse # SA SR Wp,A Wp,R SA SR Max-Min SA SR Max-Min Option 1 0 0 0.86 0.14 0+(1/0.86) = 1.16 0 1.16-0 = 1.16 0 0+(1/0.14) = 7.14 7.14-0 = 7.14 2 1.16 0 0.29 0.71 1.16+(1/0.29) = 4.61 0 4.61-0 = 4.61 0 0+(1/0.71) = 1.41 1.41-0 = 1.41 3 1.16 1.41 0.57 0.43 1.16+(1/0.57) = 2.91 1.41 2.91-1.41 = 1.77 1.16 1.41+(1/0.43) = 3.74 3.74-1.16 = 2.58 4 2.91 1.41 0.29 0.71 2.91+(1/0.29) = 6.36 1.41 6.36-1.41 = 4.95 2.91 1.41+(1/0.71) = 2.82 2.91-2.82 = 0.09 5 2.91 2.82 0.57 0.43 2.91+(1/0.57) = 4.66 2.82 4.66-2.82 = 1.84 2.91 2.82+(1/0.43) = 5.15 5.15-2.91 = 2.24 6 4.66 2.82 0.29 0.71 4.66+(1/0.29) = 8.11 2.82 8.11-2.82 = 5.29 4.66 2.82+(1/0.71) = 4.23 4.66-4.23 = 0.43 7 4.66 4.23 0.86 0.14 4.66+(1/0.86) = 5.82 4.23 5.82-4.23 = 1.59 4.66 4.23+(1/0.14) = 11.37 11.37-4.66 = 6.71
Table 8: Hypothetical trace of Event-Type selection for one Stream of the grid shown in Figure 3, based on the productions listed in Table 6.
Table 8 references a number of variables which require definition:
- The statistic SA tracks “Attack” usage within the current Stream. The statistic SR tracks “Rest” usage.
- Ap represents the “accent” associated with Pulse p. For the purposes of this demonstration, Ap is always 1.
- Wp,E represent the weight associated with Event Type E during Pulse p. These weights are specified in For examples, W1,A will be 0.86 and W1,R will be 0.14.
SA and SR are initially zero. When Event Type E is selected for Pulse p within the current Stream, the corresponding statistic advances to reflect that usage:
If the values SR and SR are close together, usage is said to be “in balance” The event engine prioritizes Event Type options based on what the statistics will become if each particular option is selected. For Pulse #1, selecting “Attack” will change SA to 1.16 while SR will remain at 0. By contrast, selecting “Rest” will leave SA at zero while changing SR to 7.14. Since selecting the “Attack” option produces the smaller difference between SA and SR (notice the Max-Min value 1.16, highlighted in blue), “Attack” is the favored option. Thus the process continues for the remaining 6 Pulses.
Problem-Level Heuristics
Each time the event engine advances to a new pulse, it applies problem-level heuristics to determine the sequence order of decisions applying to that pulse. The order is important because earlier decisions in the sequence are least fettered by constraints. (For example, if the limit on the number of simultaneous attacks is 1 and the first decision for a pulse is inclined to attack, the engine will be disposed to satisfy that inclination If the second decision is inclined to attack, the engine will be unsympathetic.) If some of the Streams are doing less well than the others at keeping Event Types in balance, then it makes sense to give these Streams the opportunity to redress the issue. The imbalance of a Stream may be quantified by evaluating the stream's running balances, determining the maximum and minimum values, and then subtracting the minimum from the maximum. This value allows the decisions to be sorted so that the greatest imbalances may be addressed first.

Figure 4: Four solutions to the Stream/Pulse grid shown in Figure 3 using the Grammar detailed in Table 6. Each solution was obtained using a different random seed.
Additional problem-level heuristics apply when Event Type biases come into play.
Sound Engine
Expressed in the jargon of my production framework, the sound engine stands as the second of two stages. The sound engine employs a “Beauty Contest” strategy, i.e. heuristic selection without constraints or backtracking. There is one problem, embracing all of the notes generated during the previous stage (that is, by the event engine). The decisions comprising this problem are the acts of selecting Sounds for notes.
The “Beauty Contest” decision strategy accomodates productions, decision-level heuristics, and problem-level heuristics, but not constraints. For the Complementary Rhythm Generator applet, the productions simply iterate through the Sounds defined for the relevant Stream.
The problem-level heuristics come down simply to presenting the notes in time order. If two or more notes begin in the same Pulse, then the order of notes is random.
The sound engine's decision-level heuristics employ statistical feedback to balance Chroma usage. When three or more Sounds are available to a Stream, then steps are taken to discourage the same Sound from occurring twice consecutively in the same Stream.
Scenario #1: Stratified Rhythms
This first scenario introduces a Grammar which offers only Hobson's Choice.
Event-type choices are entirely determined by Stream and Beat Type,
leaving absolutely no discretion to the event engine.
To run this scenario, first acquire a local copy of Rhythm-Scenario01.xml and
load this copy into the Applet.
How to do this is explained by the Instructions.
The goal of this scenario is to generate a texture from the metric framework shown in Table 3 using the ensemble of pitched percussion sounds listed in Table 9.
Stream # Instrument Pitches 1 Tubular Bells F#5 G5 A5 2 Steel Drums C5 D5 Eb5 3 Electric Piano F4 Ab4 Bb4 4 Timpani B2 C#3 E3
Table 9: Streams for Scenario #1.
The texture of the present scenario evokes the stratified style of Figure 1. During the content measures, the steel drums will play all sixteenth notes; the timpani will play all eighth notes; the electric piano will play all quarter notes; and the tubular bells will play all half notes. During the cadence measure, all instruments will converge on a down-beat half note.
The file Rhythm-Scenario01.xml is configured with the three basic Event Types listed in Table 4.
However this scenario employs just two of these basic Event Types: “Attack” ( ) and “Tie” (
) and “Tie” ( ).
“Rest” is included in the configuration because the file requires each Event-Type category to be represented.
).
“Rest” is included in the configuration because the file requires each Event-Type category to be represented.
Stream Beat Type Event Type Weight #1 (Bells) 16 Tie 1 16* Tie 1 8 Tie 1 8* Tie 1 Q Tie 1 M Attack 1 #2 (Steel Drums) 16 Attack 1 16* Attack 1 8 Attack 1 8* Attack 1 Q Attack 1 M Attack 1 #3 (Electric Piano) 16 Tie 1 16* Tie 1 8 Tie 1 8* Tie 1 Q Attack 1 M Attack 1 #4 (Timpani) 16 Tie 1 16* Tie 1 8 Attack 1 8* Attack 1 Q Attack 1 M Attack 1
Table 10: Content Grammar for Scenario #1.
The event-type nominating Grammar detailed in Table 10 applies to the content measures (1-4), while the Grammar detailed in Table 5 applies to the cadence measure (5).
To understand how the Grammar nominates an Event Type, consider the event for Stream #1 at Pulse #3.
- Referencing Table 3, the Beat Type for Pulse #3 is “8*” (“Initial Eighth”).
- Of the productions listed in Table 7, only line 4 satisfies both the Stream and Beat Type conditions.
-
Therefore “Tie” (
 ) will be the only Event Type nominated.
) will be the only Event Type nominated.
The Weight associated with each production controls the proportion of usage. This value is only meaningful when two or more productions satisfy the same conditions. Since each different set of conditions in Table 7 nominates a single Event Type (Hobson's Choice), all productions specify unit weights. (Productions offering multiple choices will be explored in Scenario #2.)
Neither heuristics nor constraints contribute significantly to Scenario #1. Heuristics do not apply because the Grammar detailed in Table 10 nominates only one Event Type for any given Stream and Beat Type. Although the “Tie” Event Type observes a no-ties-following-rest constraint, but this never comes into play because the Grammar never produces rests. Likewise for the lower and upper limits constraining the number of simultaneous attacks. These limits derive from the proportions of nominated Event-Type weights, but with no alternatives the proportions always resolve to unity. Thus the actual number of attacks will always coincide precisely with both limits.
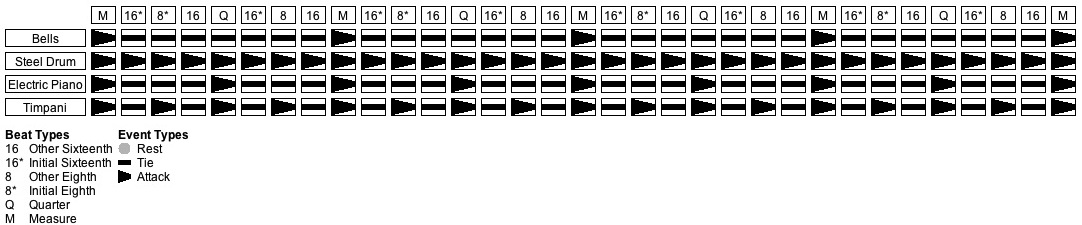
Figure 5: Stream/Pulse grid for Scenario #1.
Figure 5 demonstrates visually that the generated texture rhythmically conforms to the behavior goals stated at the outset of Scenario #1. If you want to hear a MIDI realization of this texture, you have to run the scenario.
Scenario #2: Mixed Rhythms
This second scenario explores a Grammar which nominates multiple Event Types for single
conditions.
Opening things up in this way brings production weights into play.
It also grants discretion to the event engine, which now has the ability to consider alternate solutions.
To run this scenario, first acquire a local copy of Rhythm-Scenario02.xml and
load this copy into the Applet.
How to do this is explained by the Instructions.
The goal of this scenario is to generate a texture from the metric framework shown in Table 3 using string arco sounds interleaved with string pizzicato sounds sounds. Within this texture, Beat Types “16” and “16*” produce one attack, Beat Types “8” and “8*” produce two attacks, Beat Type “Q” produces three attacks, and Beat Type “M” produces four attacks. Which Streams receive attacks during a Pulse is left to the event engine, but the engine uses this discretion to distribute attacks fairly among Streams.
Stream # Instrument Pitches 1 Violin 1 (arco) F#5 G#5 A5 B5 2 Violin 2 (pizz) B4 C5 D5 Eb5 3 Viola (arco) D4 F4 Gb4 Ab4 4 Cello (pizz) F2 G2 A2 Bb2
Table 11: Streams for Scenario #2.
The four Streams are listed in Table 8. The Event Types are the basic “Attack” and “Tie” listed in Table 4.
Stream Beat Type Event Type Weight All 16 Tie 3 Attack 1 16* Tie 3 Attack 1 8 Tie 2 Attack 2 8* Tie 2 Attack 2 Q Tie 1 Attack 3 M Tie 4
Table 12: Content Grammar for Scenario #2.
The Event-Type nominating Grammar detailed in Table 12 applies to the content measures (1-4), while the shared Grammar detailed in Table 3 applies to the cadence measure (5). Let us walk again through the selection process to see how things are changed by multiple Event Types. Consider Stream #1 at Pulse #3. The Beat Level for Pulse #3 is “8*”.
-
First to productions.
The event engine must determine which Event Types to consider.
This being a content measure, we consult the productions listed in (Table 8).
This time, both lines 7 and 8 satisfy all conditions.
Line 7 will nominate “Tie” (
 ) with weight 2 while line 8 will nominate “Attack” (
) with weight 2 while line 8 will nominate “Attack” ( ) with weight 2.
) with weight 2.
- Second to decision-level heuristics, the event engine must determine which candidates should be considered in which order. This sort order is determined by statistical feedback so that the Event Types lagging farthest behind their fair share receive first preference.
- Third to the constraints, which the candidate must satisfy. We saw previously that the lower and upper attack limits for a pulse are calculated by adding together the relative attack weights for all Streams and rounding the result. The relative attack weight in line 7 of Table 8 is (2/4). Summing four Streams gives 4 times (2/4) = 2. Rounding down gives a lower limit of 2, while rounding up gives an upper limit of 2. Although the event engine has no discretion over the total number of attack events, there are 6 different ways of distributing 2 attacks among four Streams.
- Fourth to the problem-level heuristics, which were described earlier.
Remember that neither heuristics nor constraints contribute significantly to Scenario #1. This time around, however, the event engine often faces situations where the heuristics favor options that the constraints reject. In these circumstances, the engine has no recourse but to consider less-favored options or even to go back and change earlier decisions.
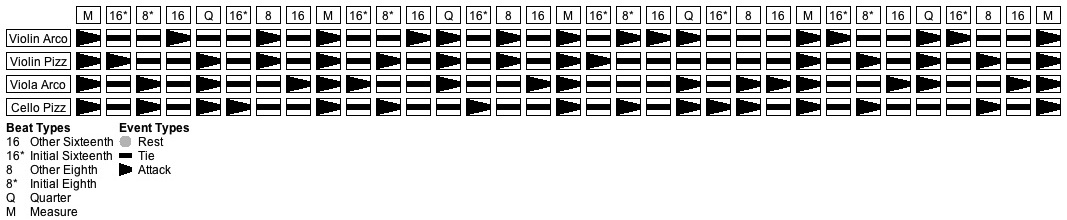
Figure 6: One of many Stream/Pulse-grid solutions for Scenario #2.
Figure 6 presents a Stream/Pulse grid generated from the common metric framework shown in Table 3 by applying the content Grammar from Table 8 to the content measures (1-4) and the cadence grammar from Table 3 to the cadence measure (5).
Scenario #3: Interlaced Rhythms
This third scenario introduces multi-tiered grammars.
It also shows how target beat levels can be used to restrict the end-points of event-type periods.
To run this scenario, first acquire a local copy of Rhythm-Scenario03.xml and
load this copy into the Applet.
How to do this is explained by the Instructions.
The goal of this scenario is to generate a texture from the metric framework shown in Table 3 using four percussion streams. These four streams are listed in Table 9. Three out of the four streams have one sound only; the tom-toms have low, medium, and high drum sizes.
Stream # Instrument Pitches 1 Cowbell 2 Claves 3 Hand Clap 4 Tom Toms High Mid Low
Table 13: Streams for Scenario #3.
As with Scenario #1, the texture will layer sixteenth-note, eighth-note, quarter-note, and half-note motions. However here in Scenario #3 the rates of motion pass between streams in a hierarchical manner:
- During any given measure (starting with Beat Type “M”), one of the streams will hold a half note.
- During the first or second quarter note of a measure (starting with Beat Types “Q” and “M”), one of the streams will hold a quarter note.
- During the first, second, third, and fourth eighth notes of a measure (starting with Beat Types “8”, “8*”, “Q”, and “M”), one of the streams will hold an eighth note.
- During every pulse in a measure (all Beat Types), one of the streams will hold an sixteenth note.
Category Name Description Icon(s) Source
Beat TypesTarget
Beat TypesREST R Rest All All TIE - Tie 



All All ATTACK A Attack All All S Sixteenth-Note Motion All All I Eighth-Note Motion 8, 8*, Q, M 8, 8*, Q, M Q Quarter-Note Motion Q, M Q, M H Half-Note Motion M M
Table 14: Event Types for Scenario #3.
The Event Types include the basic “Attack” and “Tie” described in Table 4, plus the four new “Motion” types listed in Table 15. Notice that these new Event Types list specific Source Beat Type and Target Beat Type values. Source beat types are redundant with the Beat Type production conditions. Although source beat types do not enhance functionality, they do provide a consistency check. Target beat levels, on the other hand, prolong an Event-Type period until a specified condition is satisfied.
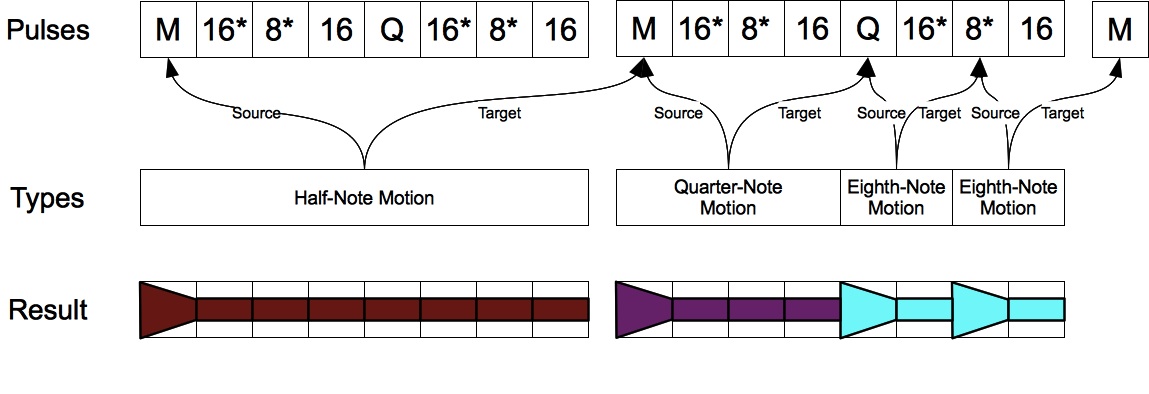
Figure 7: Event Type Sources and Targets.
Figure 7 illustrates the operation of “Source Beat Level” and “Target Beat Level” values. Notice that the target Pulse is not part of the Event-Type period, but is rather the next Pulse after.
- Having Beat Type “M” as its only source, a “Half-Note Motion” event may only fall on the downbeat of a measure. Having Beat Type “M” as its only target, an Event-Type period beginning with “Half-Note Motion” must sustain through the remainder of the measure.
- “Quarter-Note Motion” aligns with the quarter-note divisions of the measure. It may fall on either the downbeat (Beat Type “M”) or the upbeat (Beat Type “Q”), and must sustain through the quarter.
- “Eighth-Note Motion” similarly aligns with the eighth-note divisions of the measure.
Stream Beat Types Production
Event TypeWeight All 16, 16* Sixteenth-Note Motion 1 16, 16* Tie 

3 8, 8* Sixteenth-Note Motion 1 8, 8* Eighth-Note Motion 1 8, 8* Tie 
2 Q Sixteenth-Note Motion 1 Q Eighth-Note Motion 1 Q Quarter-Note Motion 1 Q Tie 1 M Sixteenth-Note Motion 1 M Eighth-Note Motion 1 M Quarter-Note Motion 1 M Half-Note Motion 1
Table 15: First tier of content Grammar for Scenario #3.
The content Grammar for Scenario #3 is all of a piece, but it makes for clearer understanding if we consider the first-tier and second-tier productions separately. Table 15 lists the first-tier productions. Notice that the Event-Type weights sum to the number of streams (4) for each set of conditions. This is done for clarity. On the downbeat (Beat Type “M”) all four motions have equal weight. On the upbeat (Beat Type “Q”), the weight previously allotted to “Half-Note Motion” has shifted over to “Tie”. For the second (Beat Type “8*”), and fourth eighth note (Beat Type “8”), the weight previously allotted to “Quarter-Note Motion” also shifts over to “Tie”. For Beat Types “16*” and “16” only “Sixteenth-Note Motion” is available.
Stream Beat Types Context
Event TypeProduction
Event TypeWeight All 16, 16* Sixteenth-Note Motion Attack 1 16, 16*, 8, 8*, Q, M Sixteenth-Note Motion Attack 1 16, 16* Eighth-Note Motion Tie 1 8, 8*, Q, M Eighth-Note Motion Attack 1 16, 16*, 8, 8* Quarter-Note Motion Tie 1 Q, M Quarter-Note Motion Attack 1 16, 16*, 8, 8*, Q Half-Note Motion Tie 1 M Half-Note Motion Attack 1
Table 16: Second tier of content Grammar for Scenario #3.
Table 16 lists the second-tier productions of the content Grammar. For a second-tier production to comply, it is necessary to satisfy not just the Stream and Beat Type, but also the Context Event Type, which must match the Production Event Type from the previous tier. For example, the Beat Type for Pulse #4 is “16” and the first-tier choice for Stream #2 (Claves) during Pulse #4 is “Tie”. The engine scans backward to the initiating event; this happens at Pulse #3 where the choice is “Eighth-Note Motion”. The only line in Table 14 that satisfies Stream #2, Beat Type “16”, and Context Event Type “Eighth-Note Motion” is line #2. This line therefore nominates “Tie” with weight 1.
Separating the tiers in this manner suggests that the event engine takes one pass through the grid to generate this information and a second pass through the intermediate choices to generate the final result. In fact the event engine augments the grid with four “Meta” Streams. When the engine advances into a new Pulse, it handles the four first-tier (“Meta”) cells as a group with its own decision-level heuristics. After all four “Meta”Event Types have been selected, the engine then procedes to resolve the regular Streams events.
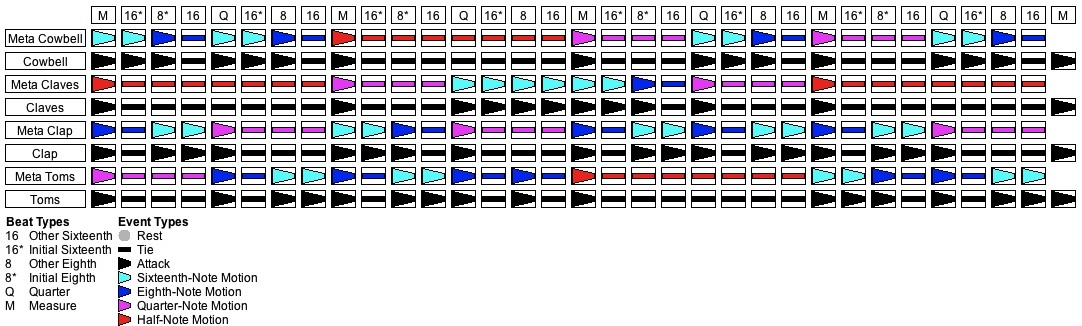
Figure 8: One of many Stream/Pulse-grid solutions for Scenario #3.
Figure 8 presents a Stream/Pulse grid generated from the common metric framework shown in Table 3 by applying the double-tier content Grammar (Table 15 and Table 16 combined) to the content measures (1-4) and the single-tier cadence Grammar from Table 3 to the cadence measure (5).
Scenario #4: Roles
This fourth scenario continues multi-tiered Grammars.
To run this scenario, first acquire a local copy of Rhythm-Scenario04.xml and
load this copy into the Applet.
How to do this is explained by the Instructions.
The goal of this scenario is to generate a texture from the metric framework shown in Table 3 using keyboard and mallet sounds. Table 17 provides the stream details.
Stream # Instrument Pitches 1 Harp F5 G5 A5 B5 2 Vibraphone B4 C5 D5 E5 3 Harpsichord D4 F4 G4 A4 4 Marimba G3 A3 B3 C4
Table 17: Streams for Scenario #4.
The streams will modulate at the barline between a “Sixteenth Motion” role and an “Eighth Motion” role. The “Sixteenth Motion” role permits attacks everywhere. The “Eighth Motion” role only permits attacks on the eighth-note divisions of the measure.
Category Name Description Icon Source
Beat LevelsTarget
Beat LevelsREST R Rest All All TIE - Tie 

All All ATTACK A Attack All All S Sixteenth Motion M M I Eighth Motion M M
Table 18: Event Types for Scenario #4.
The Event Types are listed in Table 18. Notice that the source and target for “Sixteenth Motion” and “Eighth Motion” are both fixed at “M”, the downbeat.
Stream Beat Type Production
Event TypeWeight All 16, 16*, 8, 8*, Q 
1 M Sixteenth Motion 2 M Eighth Motion 2
Table 19: First-tier content Grammar for Scenario #4.
Table 19 lists the first-tier productions. At beat level 5, “Sixteenth Motion” and “Eighth Motion” each have weight 2 out of a total of 4. This means that on the downbeat, the event engine will select “Sixteenth Motion” for two streams and “Eighth Motion” for the remaining two streams.
Stream Beat Types Context
Event TypeProduction
Event TypeWeight All 16, 16*, 8, 8*, Q Sixteenth Motion Attack 2 16, 16*, 8, 8*, Q Sixteenth Motion Tie 1 M Sixteenth Motion Attack 1 16, 16* Eighth Motion Tie 1 8, 8*, Q Eighth Motion Attack 2 8, 8*, Q Eighth Motion Tie 1 M Eighth Motion 
Attack 1
Table 20: Second-tier content Grammar for Scenario #4.
Table 20 lists the second-tier productions of the content Grammar. “Sixteenth Motion” and “Eighth Motion” downbeats both require attacks. Productions for the “Sixteenth Motion” nominate attacks and ties at all other beat levels in a proportion of two attacks for every one tie. Productions for the “Eighth Motion” nominate only ties for Beat Types “16” and “16*”, which are the sixteenth-note offbeats. There are separate “Eighth Motion” productions for Beat Types “8”, “8*”, and “Q” which are the eighth-note divisions of the measure excluding the downbeat. For these beat levels the “Eighth Motion” proportion is two attacks for every one tie.
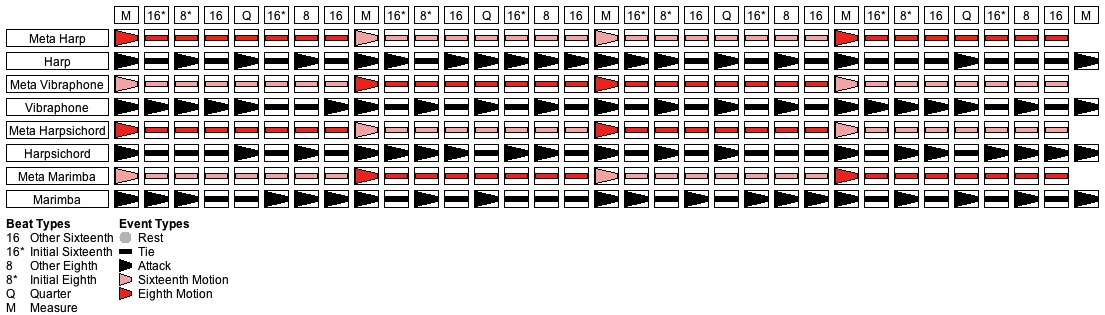
Figure 9: One of many Stream/Pulse-grid solutions for Scenario #4.
Figure 9 presents the final stream/pulse grid generated from the common metric framework shown in Table 3 by applying the content Grammar (Table 18 and Table 20 combined) to the content measures (1-4) and the cadence Grammar from Table 3 to the cadence measure (5). Let's just verify the balances for Stream #1 (Harp). Looking back at Table 19, Stream #1 assumes the “Sixteenth Motion” role in measures 1 and 3 and the “Eighth Motion” role in measures 2 and 4. Coming back to Table 21, the number of Harp attacks in measures 1 and 3 combined, excluding the downbeats, is 9 compared to 5 ties. The number of attacks is just one short of ideal. For the Harp in measures 2 and 4, considering the eighth-note divisions of the measure but not the downbeat, the number of attacks is 5, compared to 1 tie. Not great, but reasonable when one considers that the shortfall of “Sixteenth Motion” attacks would have influenced the “Eighth Motion” choices.
Scenario #5: Leading Rhythms
This fifth scenario returns to single-tiered grammars, but the principles
involved will shortly be used to organize groups of notes.
The scenarios up to this point have been concerned primarily with the placement of note attacks.
Here concern expands to include note durations.
To run this scenario, first acquire a local copy of Rhythm-Scenario05.xml and
load this copy into the Applet.
How to do this is explained by the Instructions.
Stream # Instrument Pitches 1 Flute F#5 G5 A5 2 Oboe C5 D5 Eb5 3 Clarinet F4 Ab4 Bb4 4 Bassoon B2 C#3 E3
Table 21: Streams for Scenario #5.
Scenario #5 begins with the metric framework shown in Table 3. Table 21 lists the streams.
Category Name Description Icon Requires
LeaderRequires
TrailerSource
Beat TypesTarget
Beat TypesREST R Rest All All TIE - Tie 


Yes All All A S Attack All All ATTACK S On-Beat Short M 8* L On-Beat Long Yes M M U Off-Beat Long Yes 8* M
Table 22: Event Types for Scenario #5.
The object of this scenario is to generate a texture that moves at the pace of the bar line. Instruments (streams) enter and leave so that, three of the four instruments are typically sounding at any given time. Table 22 lists the Event Types.
The placement of Event Types in the ATTACK category is limited to the downbeat (Beat Type “M”) and to the first eighth note after the downbeat (Beat Type “8*”). Within any measure, a stream can behave in five ways:
Play a short note on the downbeat, then rest. This behavior either creates an isolated note, or completes a phrase already in progress. Hold a note through the entire measure. This behavior can either begin initiate a new phrase or continue a phrase already in progress. Rest for an eighth note; start a note on the first eighth note after the downbeat and hold the note through the measure. This behavior initiates a new phrase with a pick-up note. Play a short note on the downbeat; start a second note on the first eighth note after the downbeat and hold the second note through the measure. Depending on other factors, this behavior either continues an existing phrase or terminates an old phrase and initiates a new phrase. (Other factors include pitch; for example, a leap between the two notes supports the second interpretation.) Rest for the entire measure.
Notice in Table 22 that the “On-Beat Long” and “Off-Beat Long” event types both require trailers. Engaging this feature activates a constraint that prevents the event engine from resting after an “On-Beat Long” or “Off-Beat Long” note.
This, for those of you who do not understand already, is one reason why duration contributes actively to musical rhythm. Duration is one of the primary factors signaling phrase continuation.
Stream Beat Types Context Event Type Weight All 16, 16*, 8 Rest 1 Tie 
3 8* Rest 1 Tie 2 Off-Beat Long 1 Q Rest 1 Tie 
3 M Rest 1 On-Beat Short 1.5 On-Beat Long 1.5
Table 23: Content Grammar for Scenario #5.
Table 23 formally lays out the content Grammar for Scenario #5. The productions in this Grammar act together with the special attributes of “On-Beat Short”, “On-Beat Long”, and “Off-Beat Long” to generate a texture which behaves as described above. Take special notice of the fact that each set of conditions assigns 1/4 of the weight to rests and 3/4 of the weight to non-rests.
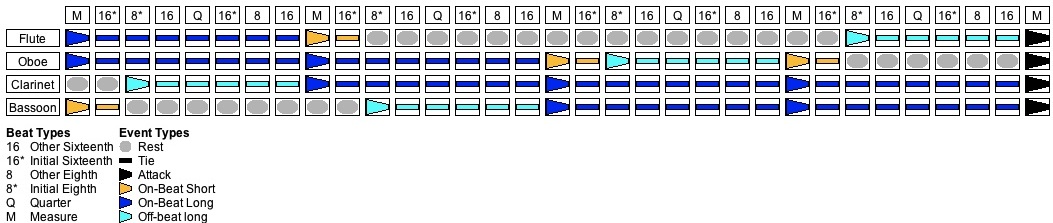
Figure 10: One of many Stream/Pulse-grid solutions for Scenario #5.
The results shown in Figure 10 were generated from the metric framework shown in Table 3 by applying the content Grammar from Table 24 to the content measures (1-4) and by applying the cadence Grammar from Table 3 to the cadence measure (5).
Scenario #6: Leading Phrases
Scenario #6 synthesizes the phrase behaviors of Scenario #5 with the tiered roles of
Scenario #4. In this last scenario, the single notes produced by “On-Beat Long”
and “Off-Beat Long” Event Types of Scenario #5 divide
into note sequences.
To run this scenario, first acquire a local copy of Rhythm-Scenario06.xml and
load this copy into the Applet.
How to do this is explained by the Instructions.
Scenario #6 begins with the metric framework shown in Table 3. It repeats the streams used in Scenario #5 and listed in Table 21. It also employs the Event Types listed in Table 22.
Stream Beat Types Context Production
Event TypeWeight All 16, 16*, 8 1 Tie 
3 8* Rest 1 Tie 2 Off-Beat Long 1 Q Rest 1 Tie 
3 M Rest 1 On-Beat Short 1.5 On-Beat Long 1.5
Table 24: First tier content Grammar for Scenario #6. Adapted from Table 23 using the Event Types listed in Table 22.
Table 24 converts the single-tier grammar from Scenario #5 into a top-tier grammar for Scenario #6.
Stream Beat Types Context
Event TypeProduction
Event TypeWeight All All Rest Rest 2 16, 16*, 8, 8*, Q On-Beat Short Tie 2 M On-Beat Short Attack 2 16, 16*, 8, Q Off-Beat Long Attack 2 16, 16*, 8, Q Off-Beat Long Tie 1 8* Off-Beat Long Attack 2 8* Off-Beat Long Tie 1 16, 16* On-Beat Long Tie 1 8, 8*, Q On-Beat Long Attack 2 8, 8*, Q On-Beat Long Tie 1 M On-Beat Long Attack 1
Table 25: Second-tier content Grammar for Scenario #6. Adapted from Table 20 by substituting Event Types listed in Table 22.
Table 25 lists the second-tier productions of the content Grammar. Of the contexts, “Rest” and “On-Beat Short” pass down to the lower tier. “Off-Beat Long” generates a pick-up rhythm which behaves like the “Sixteenth-Note Motion” role in Scenario #4. “On-Beat Long” generates a continuance rhythm which behaves like the “Eighth-Note Motion” role in Scenario #4. Thus pick-up rhythms are pulled into the foreground by greater activity, while continuance rythms are pushed into the background by lesser activity.
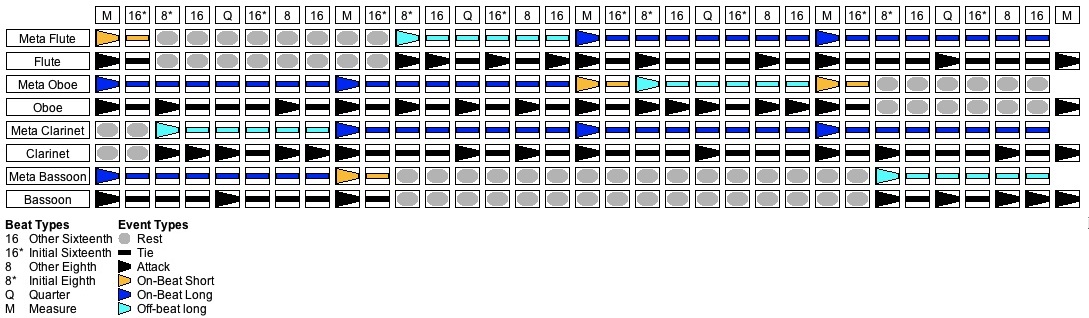
Figure 11: One of many Stream/Pulse-grid solutions for Scenario #6.
The results shown in Figure 11 were generated from the metric framework shown in Table 3 by applying the double-tier content Grammar (Table 24 and Table 25 combined) to the content measures (1-4) and the single-tier cadence Grammar from Table 3 to the cadence measure (5).
Afterword
The process here described is very complicated, but no more complicated than what human composers do with meter. The decision engines and statistical feedback, which together contribute much to that complexity, are implemented in class libraries that are shared with other compositional phases — most notably pitch selection. Yet even with these components taken off the shelf, the task of generating a texture still remains formidable. Most daunting is the business of compiling all the decisions and of organizing the decisions into schedules so that the question of which decision to attempt next can be addressed dynamically.
In Scenario #1, Scenario #2, and Scenario #5, one-tiered decision hierarchies were implemented as a root element with four stream-element members. In Scenario #3, Scenario #4, and Scenario #6, two-tiered decision hierarchies were implemented as a root element with one group-element member. This group element had four stream-element members. As of this writing I have not employed three-tiered decision hierarchies. However, the software is capable of handling any number of tiers, and a three-tiered hierarchy makes sense if one needs to handle multiple choirs of instruments. I plan to pursue that challenge very shortly.
| © Charles Ames | Page created: 2013-12-16 | Last updated: 2015-08-25 |





