Demonstration 2
Random Selection

Introduction

Demonstration 2 provided the practical component for Chapter 4: “Random Selection I — Direct Randomness” of my unpublished textbook on composing programs. It illustrates the use of random decision-making to compose a piece of music. Like its predecessor, Demonstration 2 has a tiered structure in which phrases occupy an intermediate level between the piece as a whole and the local details. From this point on, however, all resemblance ceases. Where the compositional directives for Demonstration 1 completely describe the musical results, direct compositional control over Demonstration 2 is limited to specifying a supply of options for each musical attribute involved and to prescribing a statistical distribution for each supply. All further decision-making at both intermediate and local levels of structure is delegated to the random-number generator.

From the perspective of my production framework, the process as a whole interleaves decisions about phrase attributes with decisions about note attributes. In this case each attribute is drawn from a fixed supply of options, and each supply is associated with a distribution.

Like supplies, distributions can be either discrete or continuous. A discrete distribution is set of non-negative weights or probabilities, one for each option in the supply. These values suggest in what proportions the options should be present within the outcomes of the selection process. For our purposes the distinction between weights and probabilities is that probabilities together sum to unity.

At the heart of random decision making is an engine called the random number generator. The FORTRAN language implements random generation through its built-in RANF function. This function produces a sequence of numbers which — over the long term — are uniformly distributed over the range from zero to unity. Given this function's nominal uniformity, output from RANF can be conformed to any desired distribution using an appropriate statistical transform. For discrete distributions, such a transform involves dividing the range from zero to unity into regions sized according to the distribution probabilities. Weighted random selection then comes down to generating a RANF chooser, then locating which region contains the chooser.

The rub is that patternlessness, rather than statistical conformity, is the essence of randomness. Think of it this way: if you make eight coin tosses in a row, then the outcome might be HTHTTHHT, but it might also be HHHHHHHH. In fact, these two outcomes are equally likely! Its just that there are many other outcomes mixing H's and T's but only this one way of producing only H's. The nature of randomness is also expressed in the gambler's fallacy, from which follows that if a process strives for statistical balance in the short term, then it's not random. RANF is very good at random but less good at balance.

Compositional Directives

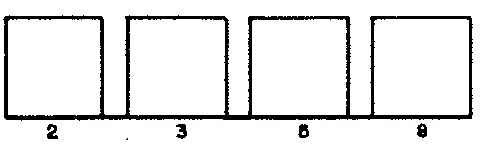
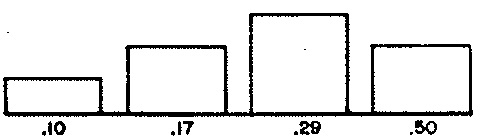
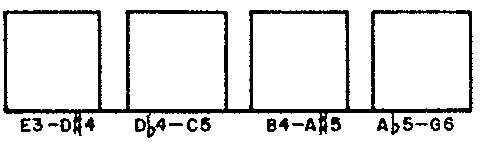
We may regard each phrase of Demonstration 2 as a chain of consecutive rhythmic ‘units’, where an individual unit can be either a note or a rest. Phrases are distinguished by four randomly selected attributes. The distribution for phrase lengths appears in Figure 1 (a). The distribution for average note durations (equivalently, average tempo) appears in Figure 1 (b). The distribution for phrase articulations appears in Figure 1 (c). The distribution for phrase registers appears in Figure 1 (d).

Articulations express the probability that a rhythmic unit within the current phrase will be a rest instead of a note; however, this probability is subject to a constraint against two consecutive units being rests. If the unit is a rest, then its duration will center around an average half as long as the average duration characterizing notes. Two consecutive notes with no intervening rest are slurred; two consecutive notes separated by a rest of null duration are tounged.

For the purposes of Demonstration 2, ‘register’ indicates a gamut of twelve adjacent semitones which holds fixed through a phrase. If the unit is a pitch, then the program first selects one of the twelve chromatic degrees and next places this degree within the appropriate register.

Figure 2 (a) depicts the exponential distribution used to select durations for notes. Rests are half as long. Figure 2 (b) depicts the discrete uniform distribution used to select chromatic degrees for notes.

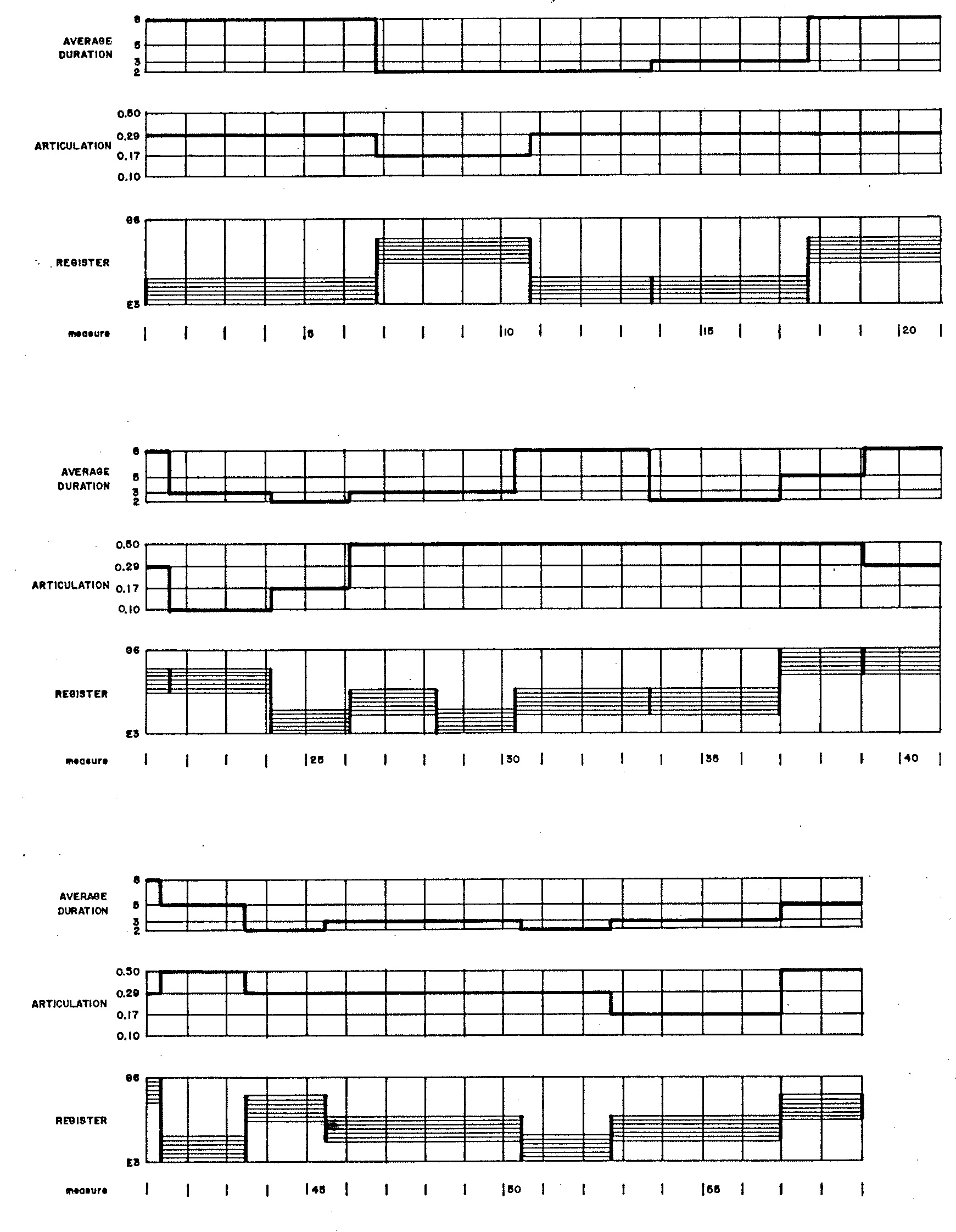
Attributes selected for phrases are depicted graphically in Figure 3

The complete product is transcribed in Figure 4

Implementation

The explanations to follow focus variously on four musical attributes: duration, articulation, register and chromatic degree. The purpose is to tease out the strands of code that affect a particular attribute, and thus to reveal the mechanics of random selection in play. The explanations are peppered with line numbers, but you are are by no means expected to chase down every line of code. Rather, you should follow through with line numbers only when you have a specific question that the narrative is not answering.

The main program DEMO2 is presented in Listing 1. The program implements the tiered musical structure described above as a design of nested loops. The bulk of DEMO2 proper (lnes 27-41) constitutes the ‘outer’ composing loop; this loop establishes the attributes depicted in Figure 3.

Subroutine PHRASE is presented in Listing 2. At the end of each iteration of the ‘outer’ composing loop, DEMO2 calls PHRASE. This call invokes an entire cycle of iterations by an ‘inner’ composing loop (lines 5-26 of PHRASE). Each ‘inner’ iteration composes a note or rest.

The symbols of DEMO2 proper adhere to four root abbreviations identifying attributes of phrases:

1. PHR — length of phrase. Parameter MPHR fixes the number of phrase lengths at 5 (line 5); line 9 populates specific values into array VALPHR; line 10 populates the corresponding weights from Figure 1 (a) into array WGTPER, and line 12 initializes the sum of these weights into variable SUMPHR.
2. AVG — average duration of notes (equivalently, average tempo); the average duration of rests is half as large. Parameter MAVG fixes the number of average note durations at 4 (line 5); line 12 populates specific values into array VALAVG. Since the weights in Figure 1 (b) are uniform, no weight array is necessary.
3. ART — articulation, expressed as the probability that a rhythmic unit will serve as a rest. Parameter MART fixes the number of articulations at 4 (line 5); line 13 populates specific values into array VALART; line 14 populates the corresponding weights from Figure 1 (c) into array WGTART, and line 15 initializes the sum of these weights into variable SUMART.
4. REG — register, expressed as the lowest pitch in a twelve-semitone gamut. Parameter MREG fixes the number of registers at 4 (line 5); line 12 populates specific values into array VALREG. Since the weights in Figure 1 (d) are uniform, no weight array is necessary.

The methods used to implement the different random decisions vary with the distributions depicted in Figure 1. DEMO2 asks the library subroutine ALEA to select average durations (line 34) and registers (line 38). ALEA is the approriate selection method for non-sequential values with uniform weighting. PHRASE selects chromatic degrees directly by asking the library function IRND to select a uniform random integer between 1 and 12 (line 13). IRND is the approriate selection method for sequential integers with uniform weighting. DEMO2 asks the library subroutine SELECT to provide durations of phrase and probabilities of rests according to stored distributions (lines 29 and 36). SELECT is the approriate selection method for non-sequential values with nonuniform weighting. Durations for individual notes and rests follow exponential distributions provided by the library function RANX (lines 9 and 16) of PHRASE.

Subroutine PHRASE implements the note-rest loop. Line 9 decides whether the current iteration should generate a note or a rest. For notes, lines 11-15 choose the duration and chromatic degree. If rests, lines 17-22 choose the duration. The note/rest loop completes by calling subroutine WNOTE in line 25.

Rhythm

So long as no two rests occur consecutively, PHRASE settles the question of whether a rhythmic unit sould serve as a note or as a rest by asking (line 7) the library function SUCCES to conduct a Bernoulli trial.

Remember that exponentially distributed values range continously from zero (exclusive) to infinity. The variable REMAIN (lines 9-18 of PHRASE) enables PHRASE to reconcile exponentially distributed durations with the discrete rhythmic neumes of musical notation. REMAIN resembles an accumulator. Each time PHRASE computes IDUR from DUR, it stores the fractional part in REMAIN. (In line 11, the lower bound of 1 precludes generation of notes without durations. The increment of 0.5 causes PHRASE to approximate DUR as the next larger integer when its fractional part exceeds 1/2. In such cases, the amout added to REMAIN is negative.) The next time it computes DUR, PHRASE adds REMAIN to the new random value. Fractional parts of consecutive random values accumulate until their sum exceeds unit; when this happens an additional sixteenth bleeds off into IDUR.

Pitches

The tasks of subroutine WNOTE in DEMO2 differ from those if its counterpart in DEMO1 in that pitch information takes the form of a chromatic degree (1 to 12) and a register. Registers are expressed in semitones above 32' C and indicate the lower bound of the octave which is to hold the final pitch. The integer library function IOCT shown in Listing 3 performs the necessary conversion from registers to octaves.

Continuous Uniform Randomness

All of the random generators employed for these Eleven Demonstrations leverage FORTRAN's built-in RANF function. This function generates pseudorandom numbers in the real range from zero to unity using D.H. Lehmer's linear congruence algorithm.

Discrete Uniform Randomness

The library function IRND¹ generates random integers in the range from 1 to NUM, the function's sole argument. NUM must be a positive integer.

IRND evaluates the formula IFIX(RANF()*FLOAT(NUM)) + 1. In this formula, IFIX converts a real argument to the greatest integer less than or equal to the argument, while FLOAT converts an integer argument to a real.

Mapped Discrete Uniform Randomness

The library subroutine ALEA² selects values randomly with uniform likelihood from a supply. It is modeled on the ALEA feature of G.M. Koenig's Project Two, which also contributes the term “supply”. Calls to ALEA require three arguments:

1. RESULT — ALEA selects a supply value and returns the value in this location.
2. VALUE — Supply of values. Duplicate values are not permitted. VALUE must be an array whose dimension in the calling program is NUM (argument #3 below).
3. NUM — Number of supply elements (dimension of array VALUE in the calling program).

ALEA leverages the library function IRND. It generates a random index I=IRND(NUM), then places VALUE(I) in RESULT.

Random Trials

The library function SUCCES³ returns either .TRUE. or .FALSE with probability P. It models a probabilistic scenario known as a Bernoulli Trial. P is the sole parameter.

SUCCES evaluates the logical formula RANF().LE.P.

Weighted Randomness

The library subroutine SELECT⁴ selects values randomly with nonuniform likelihood from a supply. Calls to SELECT require five arguments:

1. RESULT — SELECT selects a supply value and returns the value in this location.
2. VALUE — Supply of values. Duplicate values are not permitted. VALUE must be an array whose dimension in the calling program is NUM (argument #5 below).
3. WEIGHT — Relative weights for each value. WEIGHT must be a real array whose dimension in the calling program is NUM. Each weight must be zero or greater, and at least one weight must be positive.
4. SUM — Total of all NUM weights in the WEIGHT array. SUM must be real.
5. NUM — Number of supply elements (dimension of arrays VALUE and WEIGHT in the calling program).

SELECT operates by generating a ‘chooser’ value R=SUM*RANF(), then iterates through the WEIGHT array on index I. If WEIGHT(I).LE.R then SELECT breaks from the loop; otherwise, SELECT sets R=R-WEIGHT(I) and iterates. SELECT completes by setting RESULT=VALUE(I).

Continuous Uniform Randomness

The library function UNIFRM⁵ generates random numbers which are uniformly distributed over a continuous range. Calls to UNIFRM require two arguments:

1. A — lower bound.
2. B — higher bound.

UNIFRM evaluates the formula ((B-A)*RANF()) + B.

Negative Exponential Randomness

The real-valued library function RANX⁵ implements John Myhill's generalization of the negative exponential randomness. Pure negative exponential randomness was used to generate durations in the stochastic music program of Iannis Xenakis; it models waiting scenarios in nature such as radioactive decay. Myhills' 1979 generalization added a second parameter allowing a continuum of behaviors from strict periodicity to pure negative exponential randomness. The probability densitiy curve for negative exponential randomness appears as Figure 2 (a). Calls to RANX require two arguments:

1. AVG — Average value. AVG must be a real number in the calling program whose value is positive.
2. PROPOR — Maximum result divided by minimum result. PROPOR must be a real number in the calling program whose value is 1.0 or greater. With this argument near unity, results will cluster around AVG. As PROPOR increases, results come to resemble pure negative exponential randomness.

To learn more of the workings of negative exponential randomness and of Myhill's generalization, see the references provided.

Comments

1. Function IRND implements a direct version of the discrete uniform distribution described on page 58 of my “Catalog of Statistical Distributions”. The FORTRAN source code for function IRND appears in Automated Composition, Chapter 4, p. 4-8.
2. Subroutine ALEA implements an indirect version of the discrete uniform distribution described on page 58 of my “Catalog of Statistical Distributions”. The FORTRAN source code for subroutine ALEA appears in Automated Composition, Chapter 4, p. 4-9.
3. The Bernoulli distribution is described on page 58 of my “Catalog of Statistical Distributions”. The FORTRAN source code for function SUCCES appears in Automated Composition, Chapter 4, pp. 4-11 to 4-12.
4. My “Catalog of Statistical Distributions” generalizes the process of statistical selection by positing a continuous uniform “driver” range from zero to unity. Such values might be generating using standard linear congruence randomness, but they do not have to be. That article's section on “Discrete Distributions” (page 58) begins by describing the general approach to transforming driver values into discrete integers, working from a table of weights. The FORTRAN source code for subroutine SELECT appears in Automated Composition, Chapter 4, pp. 4-17 to 4-18.
5. Continuous uniform distribution is described on page 62 of my Catalog of Statistical Distributions. For reasons unrecalled by me the FORTRAN source code for function UNIFRM does not appear in Automated Composition.
6. The Myhill distribution is described on page 67 of my Catalog of Statistical Distributions. The FORTRAN source code for function RANX appears in Automated Composition, Chapter 4, pp. 4-20 to 4-25.