Intelligent Part Writer

Overview

This attraction demonstrates the use of a computer program to solve problems in musical voice-leading. When I say that this program is “intelligent” I simply mean that it applies techniques drawn from Artificial Intelligence — for example, in the early chess-playing and theorem-proving programs by Simon and Newell. I consider the level of expertise to be superior to that of first-year students of musical theory realizing figured-bass examples. Such students might indeed benefit from understanding how this program goes about attacking the problem, since the approach is modeled on human behavior.

I should acknowledge that the more difficult problem of harmonizing a melody was previously addressed in CHORAL, a program by Kemal Ebcioğlu who had been my colleague at the Statue University of New York at Buffalo during the late 70's and early 80's. I am not familiar with the inner workings of CHORAL, but I do know that Kemal's program succeeded in duplicating J.S. Bach's own harmonization on at least one instance.

I first developed this approach presented here as a proof of concept during the early 1980's. It was submitted to the Computer Music Journal and rejected for reasons having to do with the “hierarchy of voices”. (I still have no idea what that means.) I later put the approach to work for the Cybernetic Composer, generating background chords for the ragtime style.

Component Model

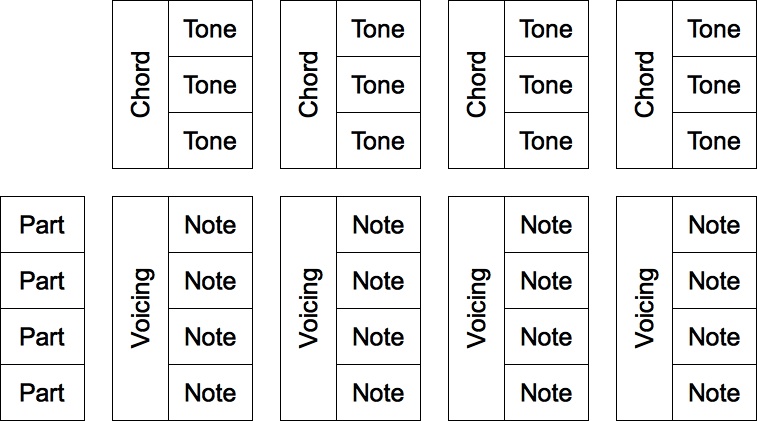
Figure 1: Voicing structure for Intelligent Part Writer documents.

The Intelligent Part Writer implements the structure shown in Figure 1. There are three top-level component types: Chords, Parts, and Voicings. Chords contain Tones (up to seven), while Voicings contain Notes (one per Part). The collection of Voicings comprises a sequence, where the duration of one Voicing determines the starting time of its successor. Chords, Tones, Parts, and Voicings are all configurable using the graphic editor. Notes are not configurable, since the whole point is for the computer to select pitches for Notes.

Expressed in the jargon of my production framework,

• The Voicing sequence is a problem implemented using a “Heuristic Search” strategy, which incorporates dependency-directed backtracking. (“Search”, “heuristics” and “backtracking” are explained below.) Each individual Voicing stands as a scaffold. Voicings are processed in time order, advancing from left to right unless an impasse is reached.
• The Notes within each Voicing stand as decisions, the options of which are pitches. There are productions which compile the lists of pitches available to each note, decision-level heuristics which determine the order in which pitches are considered, problem-level heuristics which determine the order of Notes within a Voicing, and constraints which determine if a pitch conflicts with previous choices.
• The “general” method of statistical feedback is incorporated into the production framework. Option values in the framework correspond to pitches in the part-writing engine, while states correspond to diatonic steps.

Chords and Tones

A Chord is a collection of Tones. Each tone is described by six attributes:

• Degree — Notation follows Alan Ashton's linear music code with the pound sign (#) for sharps and the exclamation point (!) for flats: C, C#/D!, E, F, F#/G!, G, G#/A!, A, A#/B!, B. Since the program strives to balance the seven diatonic steps, you may not employ any letter name more than once in a chord. For example you may employ both D natural and E flat in the same chord, but you may not employ both D natural and D sharp.
• Significance — Indicates whether the tone contributes to the peculiar flavor of the Chord. There are two values:
  • OBLIGITORY — At least one instance of the tone must be present in a voicing.
  • OPTIONAL — Presence is not required.
• Multiplicity — Indicates whether the tone may appear once, twice, or any number of times in a voicing. There are three values:
  • SINGLE — The tone may not be represented more than once in a voicing.
  • DOUBLE — The tone may not be represented more than twice in a voicing.
  • FREE — The tone may be represented any number of times in a voicing.
• Tendency — The stepwise direction by which a tone will resolve. There are four values:
  • NONE — no tendency.
  • NEUTRAL — resolves upwards or downwards by step.
  • DOWNWARD — resolves downward by step.
  • UPWARD — resolves upward by step.
• Urgency — The stepwise direction in which a tone expects to move. There are three values:
  • NONE — No urgency: used when the Tendency is NONE.
  • OPTIONAL — Optional urgency: resolution is encouraged heuristically but not enforced by constraint.
  • OBLIGATORY — Obligatory urgency: resolution is both encouraged heuristically and enforced by constraint.
• Bass Tone — This is a yes/no flag. If selected for a tone, the bass part may employ this tone only. Only one tone in a Chord may have its Bass Tone flag selected.

How tones behave depends entirely on how chords are configured in the input file. The Partwriter-Example.xml file defines seven Chords: “C Major”, “A Minor 7th”, “A Dominant 7th”, “G Dominant 7th”, “E Minor 7th”, “F Major”, and “D Minor 7th”.

Degree	Significance	Multiplicity	Tendency	Urgency	Bass Tone
C	OBLIGATORY	FREE	NONE	NONE	true
E	OBLIGATORY	SINGLE	UPWARD	OPTIONAL	false
G	OPTIONAL	SINGLE	NONE	NONE	false

Table 1-1: Tones of Chord #1: C Major.

Degree	Significance	Multiplicity	Tendency	Urgency	Bass Tone
A	OBLIGATORY	SINGLE	NONE	NONE	true
C	OBLIGATORY	FREE	NONE	NONE	false
E	OPTIONAL	SINGLE	NONE	NONE	false
G	OBLIGATORY	SINGLE	DOWNWARD	OBLIGATORY	false

Table 1-2: Tones of Chord #2: A Minor 7th.

Degree	Significance	Multiplicity	Tendency	Urgency	Bass Tone
A	OBLIGATORY	DOUBLE	NONE	NONE	true
C#	OBLIGATORY	SINGLE	UPWARD	OPTIONAL	false
E	OPTIONAL	SINGLE	NONE	NONE	false
G	OBLIGATORY	SINGLE	DOWNWARD	OBLIGATORY	false

Table 1-3: Tones of Chord #3: A Dominant 7th.

Degree	Significance	Multiplicity	Tendency	Urgency	Bass Tone
G	OBLIGATORY	FREE	NONE	NONE	true
B	OBLIGATORY	SINGLE	UPWARD	OPTIONAL	false
D	OPTIONAL	SINGLE	NONE	NONE	false
F	OBLIGATORY	SINGLE	DOWNWARD	OBLIGATORY	false

Table 1-4: Tones of Chord #4: G Dominant 7th.

Degree	Significance	Multiplicity	Tendency	Urgency	Bass Tone
E	OBLIGATORY	DOUBLE	NONE	NONE	true
G	OBLIGATORY	FREE	NONE	NONE	false
B	OPTIONAL	SINGLE	UPWARD	OPTIONAL	false
D	OBLIGATORY	SINGLE	DOWNWARD	OBLIGATORY	false

Table 1-5: Tones of Chord #5: E Minor 7th.

Degree	Significance	Multiplicity	Tendency	Urgency	Bass Tone
F	OBLIGATORY	FREE	NONE	NONE	true
A	OBLIGATORY	SINGLE	UPWARD	OPTIONAL	false
C	OPTIONAL	SINGLE	NONE	NONE	false

Table 1-6: Tones of Chord #6: F Major.

Degree	Significance	Multiplicity	Tendency	Urgency	Bass Tone
D	OBLIGATORY	SINGLE	NONE	NONE	true
F	OBLIGATORY	FREE	NONE	NONE	false
A	OPTIONAL	SINGLE	NONE	NONE	false
C	OBLIGATORY	SINGLE	DOWNWARD	OBLIGATORY	false

Table 1-7: Tones of Chord #7: D Minor 7th.

All of the chords in this example designate chord-roots as bass tones. This is however, not required. As an alternative, one could define a second-inversion chord named “C Major/G”, with the same degrees as in Table 1-1, but with G designated as the bass tone and C specified with DOWNWARD tendency and OBLIGATORY urgency.

Parts

The Partwriter-Example.xml file defines four Parts. The Parts and their attributes are detailed in Table 2.

ID	Name	Clef	Low Pitch	High Pitch	Bass Part	MIDI Program	MIDI Velocity
1	Soprano	Treble	C4	G5	false	FLUTE	90
2	Alto	Treble	G3	D5	false	CLARINET	90
3	Tenor	Treble-8	C3	G4	false	FRENCH_HORN	90
4	Bass	Bass	E2	C4	true	BASSOON	90

Table 2: Parts in Partwriter-Example.xml.

Voicings

The Partwriter-Example.xml file defines a progression of nine Voicings. The Voicings and their attributes are detailed in Table 3.

ID	Chord
1	C Major
2	A Minor 7th
3	F Major
4	G Dominant 7th
5	E Minor 7th
6	A Dominant 7th
7	D Minor 7th
8	G Dominant 7th
9	C Major 7th

Table 3: Voicings in Partwriter-Example.xml.

The Decision Engine

Figure 2 charts the flow of the Heuristic Search decision engine. Although the flow chart looks daunting, but it is actually familiar to any music student who has ever tackled a part-writing exercise.

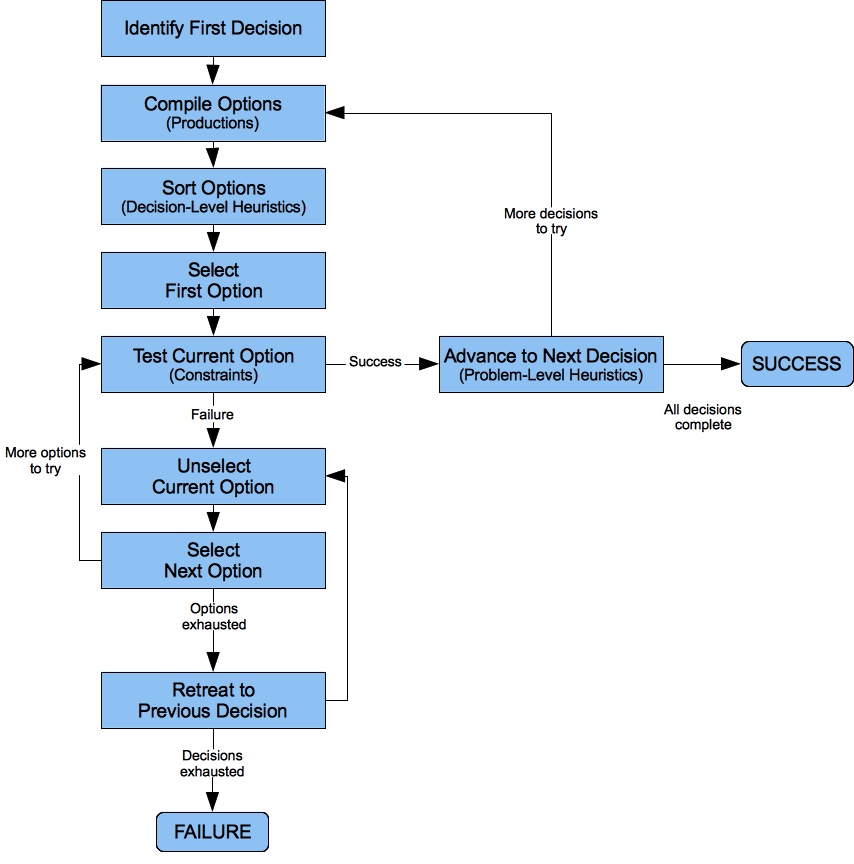
Figure 2: “Heuristic Search” decision engine.

As stated previously, a decision services a Note, while the options are pitches. I want to draw your attention to four particular elements of this flowchart:

• The element labeled Compile Options stands in for the process that nominates options for a decision.
• The element labeled Test Current Option hides the whole agony of checking to whether the pitch under consideration satifies all constraints imposed upon the selection process. The purpose of constraints is to prevent bad things from happening.
• The element labeled Retreat to Previous Decision handles the situation where none of the options available to the current decision lead to a successful solution.
• The element labeled Sort Options applies decision-level heuristics to determine the order in which pitches will be considered.
• The element labeled Advance to Next Decision applies problem-level heuristics to determine the order in which Notes will be addressed.

Productions

I have appropriated the word production to indicate a procedure which nominates pitches to be considered for a Note. (The term production comes from Noam Chomsky's generative grammars. I hope to justify this appropriation in a future attraction blending searches with grammars.) If the note's Part is other than the bass line, the productions take all the chromatic steps in the Part's range and filter these down to chord tones. For the bass line, the productions take only the chromatic steps that correspond to the bass Tone. All this happens at initialization time, before any decisions are evaluated. The filtering process just described is different from what happens with constraints If a pitch fails a constraint, the search can go back to the source of conflict and make a change. Filtered-out pitches are wrong no matter what the search does.

Constraints

The constraints imposed by the part-writing engine adapt the “Music Theory Rules” first identified by Renaissance theorists such as Gioseffo Zarlino; these rules also governed the realization of a figured bass during the Baroque period. As the Part-Writer considers pitches for notes, it identifies constraint issues in a Violations list near the bottom of the screen. Clicking on the constraint name shows you which notes are involved.

Four of the constraints enforce Tone behaviors already described. These constraints may be selectively disengaged by substituting more permissive Tone attributes.

• Resolution — Tones with OBLIGATORY Urgency must resolve stepwise according to their tendency. This constraint may be disengaged by changing the Urgency to OPTIONAL or NONE.
• Illegal Doubling — Tones with SINGLE Multiplicity may not appear more than once in a voicing. This constraint may be disengaged by changing the Multiplicity to FREE.
• Limited Doubling — Tones with DOUBLE multiplicity may not appear more than twice in a voicing. This constraint may be disengaged by changing the Multiplicity to FREE.
• Missing Obligatory Tone — Tones with OBLIGATORY Significance must appear at least once in a voicing. This constraint may be disengaged by changing the tone's Significance to OPTIONAL.

The remaining constraints enforce behaviors that are independent of Tone. These constraints may be engaged or disengaged using check boxes in the document attributes panel.

• Leap — Consecutive notes in the same part may not move by intervals of 10 or 11 semitones, or by any interval larger than an octave. This constraint is engaged by default. It may be disengaged in the document attributes panel using the Suppress Leaps check box.
• Tritone Motion — Consecutive notes in the same part may not move by intervals of 6 semitones. This constraint is engaged by default. It may be disengaged in the document attributes panel using the Suppress Tritone check box.
• Voice Crossing — As part numbers go up, part ranges go down. Therefore when this constraint is engaged, one note in a voicing may not have a higher pitch than another note with a lower part number. This constraint is engaged by default. It may be disengaged in the document attributes panel using the Suppress Voice Crossing check box.
• Unison Doubling — Two notes in the same voicing may not play the same pitch. This constraint is disengaged by default. It may be engaged in the document attributes panel using the Suppress Unison Doubling check box.
• Wide Spacing — Pitches in adjacent parts may not be separated by intervals greater than an octave. This constraint is engaged by default. It may be disengaged in the document attributes panel using the Suppress Wide Spacing check box.
• Parallel Perfect Consonances — Parts may not move in parallel perfect consonances (e.g. parallel octaves, fourths, or fifths). This constraint is engaged by default. It may be disengaged in the document attributes panel using the Suppress Parallel Perfect Consonances check box.
• Similar Motion — At least one part must either sustain its pitch or move contrary to the direction that most other parts are moving. This constraint is engaged by default. It may be disengaged in the document attributes panel using the Suppress Similar Motion check box.

Backtracking

If you have experienced part-writing, you are familiar with coming to an impasse with no recourse but to go back and change earlier decisions. The flow-chart shown in Figure 2 accommodates impasses in the same way. When a particular decision has exhausted all available options, the engine is capable of retreating to an earlier decision and taking up the next option in this earlier decision's schedule. The ability to revise earlier decisions is called backtracking. Backtracking is an essential technique from artificial intelligence. It transforms a simple process of selection into a search that continues until one of two outcomes have been reached:

• A successful solution has been discovered.
• All possible combinations have been exhausted.

The second, negative outcome is possible because once the search has rejected a certain sequence of choices, it never reattempts that sequence.

The discussion of backtracking now becomes technically complicated without providing further musical insight. You may wish to skip forward to the next topic, heuristics.

There are two kinds of backtracking, simple and dependency-directed. When I first became involved with AI search methods during the early 1980's, my programs used simple backtracking. In those days having your own microprocessor was a rare thing, but I had one. I needed it because sometimes my programs ran on for days. Every once in a while, I would check the display (something like the Part-Writer animation, but using characters) to verify that the run was making progress. And I could see the search failing to select a pitch for some current note due to a conflict with some previous note. Each time it failed it would back up one step, make a change, and try again. It was agony. It might take 15 minutes to work its way back to the source of conflict, which might itself be limited in the pitches it could consider. So it might go back further, work forward to the original source of conflict, and revert to the pitch that caused the problem in the first place.

Clearly some way needed to be found to backtrack directly to the source of conflict. I worked something out, then ran into my friend Kemal, and described what I was doing:

Oh yes. I do that. Its called dependency-directed backtracking. There's a famous article by Stallman and Sussman describing it.

Anyway, here's what the Intelligent Part Writer does to achieve dependency-directed backtracking:

• Each time a pitch fails a constraint, the constraint assesses blame. For example, if the part makes an improper leap, then the constraint blames the “from” note. If the part moves in parallel perfect consonances with another part, then the constraint blames the other part's note under the current voicing. In either case, the blamed note must be changed to render the current pitch viable.
• Each decision has a sequence number that identifies in what order the decision was processed (understand that the decision order is dynamic). As the search works through the constraints for an option, it identifies the option's source of conflict as the blamed decision with the smallest decision sequence number. For example if a pitch results both in an improper leap (blaming a note in the previous voicing) and in parallel motion (blaming a note in the current voicing), then decision blamed for the leap will be identified as the source of conflict.
• The decision engine maintains a backtracking queue listing decisions in sequence-number order. Whenever a decision exhausts its options, the decision's own sources of conflict (one for each rejected pitch) are folded into the backtracking queue.
• When time comes to backtrack, the decision with the largest sequence number is peeled off the end of the backtracking queue.

Heuristics

While a graduate student at SUNY/Buffalo, I attended composition seminars with Morton Feldman. I remember Feldman priding himself upon working in ink. Certainly for Feldman the old rules don't apply, yet he was known for coming up with the right chord for the moment. Since he composed at the piano, it is likely Feldman tried out a few wrong chords before getting to the right one, yet once that chord was chosen he never changed his mind.

Backtracking is the AI equivalent of a theory student applying a pencil eraser. The very need to backtrack exposes the inefficiency of a selection process guided exclusively by rules. Pile on that the frustration of the part-writing student whose solution is graded down for being “unmusical” even though all the rules have been observed.

As the student gains experience, he or she will come to recognize in advance that some actions will lead to success and while impasse. In particular, the order in which decisions are addressed matters greatly. For example, experience quickly reveals that if one part offers a dissonance for resolution, that's the part you want to handle first. Otherwise you waste time making choices which will conflict with the resolution pitch. Taking this further, if a second part wants to satisfy a leading tone, its best chance happens when you address this second part next after the dissonance.

Procedures which influence the order by which decisions are taken, or the order by which options are considered, are called heuristics. The purpose of heuristics is to encourage good things to happen. In contrast to algorithms, which always produce correct answers (or the conclusion that no correct answer exists) heuristics enforce no rules. Rather, heuristics promote tendencies.

Implementing heuristics is simple, at least in principle: Assign a preference value to each item, then sort the items by preference. However it gets more complicated when the preference values are multidimensional. My 1992 article “Quantifying Musical Merit” delves further into ways of calculating preference values.

Heuristics apply at two levels in Figure 2:

• The element labeled Advance to Next Decision applies heuristics at the at the problem level. The part-writing engine advances sequentially from Voicing to Voicing. Within a Voicing, the order of Notes is dynamic and the preference value ξ(n) for Note n is calculated in four steps:
  • Set ξ(n) to a value generated by Java's Random.nextDouble() method; that is, to a random number which is uniformly distributed between zero and unity. ξ(n) at this point will have random digits to the right of the decimal point and zero to the left of the decimal point.
  • If the Note is in the bass Part, increment ξ(n) by 1.
  • If the Note has a predecessor in the same Part and the predecessor Tone has OPTIONAL Urgency, increment ξ(n) by 2.
  • If the Note has a predecessor in the same Part and the predecessor Tone has OBLIGATORY Urgency, increment ξ(n) by 4.
  With preference values calculated in this manner, predecessor Urgency is the most significant criterion. Notes with urgent predecessors always trump Notes without urgent predecessors. Being in the bass is a secondary criterion; bass Notes trump non-bass Notes only when predecessor Urgencies are equal. Everything else held equal, the relative order of any two Notes is random.
• The element labeled Sort Options applies heuristics at the decision level. In the part-writing engine, this comes down to determining the order in which pitches will be considered for a Note. Preference is given to pitches which satisfy tendencies. Otherwise my technique of statistical feedback applies. Usage statistics are maintained for each of the seven diatonic scale steps, and secondary preference is given to the pitches falling farthest behind their fair share of usage.